



Next: Diskrete Zufallsvariable; Wahrscheinlichkeitsfunktion
Up: Zufallsvariable und ihre Charakteristiken
Previous: Zufallsvariable
Contents
Verteilung von Zufallsvariablen
Die Regularitätsbedingung (1) in Definition 3.1 kann durch
die folgende (scheinbar schärfere, in Wirklichkeit jedoch
äquivalente) Bedingung ersetzt werden: Für jede Zufallsvariable
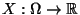 gilt
gilt
Dies führt
zu der folgenden Begriffsbildung.
- Definition 3.2
 Sei
Sei
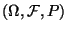 ein beliebiger
Wahrscheinlichkeitsraum, und
ein beliebiger
Wahrscheinlichkeitsraum, und
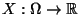 sei eine
beliebige Zufallsvariable. Die
Verteilung der Zufallsvariable
sei eine
beliebige Zufallsvariable. Die
Verteilung der Zufallsvariable  ist die Mengenfunktion
ist die Mengenfunktion
![$ P_{X}:\mathcal{B}(\mathbb{R})\rightarrow [0,1]$](img235.png) mit
mit
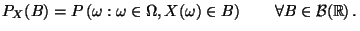 |
(2) |
- Beachte
-
- Die in (2) definierte Mengenfunktion
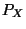 ist ein Wahrscheinlichkeitsmaß auf dem Meßraum
ist ein Wahrscheinlichkeitsmaß auf dem Meßraum
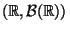 .
.
- Die Abbildung
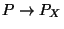 nennt man
Maßtransport vom Meßraum
nennt man
Maßtransport vom Meßraum
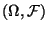 in den Meßraum
in den Meßraum
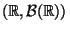 .
.
Die folgende Kurzschreibweise ist üblich:
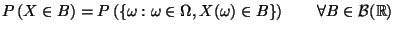
Speziell:
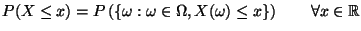
Subsections
Roland Maier
2001-08-20
![]() gilt
gilt
![]()
![]()