



Next: Beispiele
Up: Stochastische Unabhängigkeit
Previous: Unabhängige Ereignisse
Contents
Unabhängige Zufallsvariable
Die Unabhängigkeit von Zufallsvariablen wird durch die
Unabhängigkeit von Ereignissen ausgedrückt.
So heißen zwei Zufallsvariable 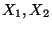 unabhängig, wenn die
Ereignisse
unabhängig, wenn die
Ereignisse
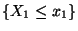 und
und
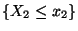 für beliebige
für beliebige
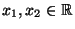 unabhängig im Sinne von Definition 3.16 sind.
unabhängig im Sinne von Definition 3.16 sind.
Für Folgen von Zufallsvariablen wird der Begriff der
Unabhängigkeit folgendermaßen gebildet.
- Definition 3.17
 Sei
Sei
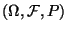 ein beliebiger
Wahrscheinlichkeitsraum.
ein beliebiger
Wahrscheinlichkeitsraum.
- Die Zufallsvariablen
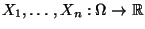 heißen unabhängig, falls
heißen unabhängig, falls
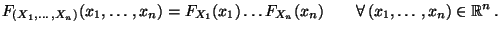 |
(19) |
- Sei
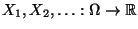 eine beliebige (unendliche) Folge
von Zufallsvariablen. Dann sagt man, daß
eine beliebige (unendliche) Folge
von Zufallsvariablen. Dann sagt man, daß
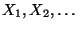 unabhängige Zufallsvariablen
sind, falls jede endliche Teilfolge
unabhängige Zufallsvariablen
sind, falls jede endliche Teilfolge
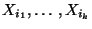 von
von
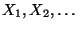 aus unabhängigen Zufallsvariablen besteht.
aus unabhängigen Zufallsvariablen besteht.
- Beachte
-
- Aus den Definitionen 3.5 und 3.7 der
Verteilungsfunktionen
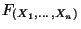 und
und
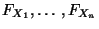 ergibt sich sofort, daß die
Definitionsgleichung (19) äquivalent ist mit
ergibt sich sofort, daß die
Definitionsgleichung (19) äquivalent ist mit
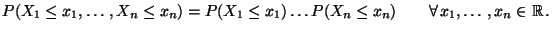 |
(20) |
- Darüber hinaus kann man zeigen, daß (20) und damit auch
(19) äquivalent ist mit
Hieraus und aus den Definitionsgleichungen (3) und
(10) der Dichten
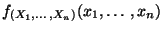 und
und
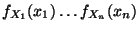 ergibt sich unmittelbar die folgende
Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.
ergibt sich unmittelbar die folgende
Charakterisierung der Unabhängigkeit von diskreten bzw.
absolutstetigen Zufallsvariablen.
- Theorem 3.18
-
- Sei
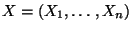 ein diskreter Zufallsvektor
mit
ein diskreter Zufallsvektor
mit
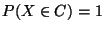 für eine abzählbare Menge
für eine abzählbare Menge
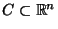 .
Seine Komponenten
.
Seine Komponenten
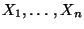 sind genau dann unabhängige Zufallsvariable, wenn
sind genau dann unabhängige Zufallsvariable, wenn
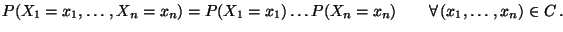 |
(21) |
- Sei
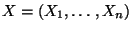 ein absolutstetiger Zufallsvektor.
Seine Komponenten
ein absolutstetiger Zufallsvektor.
Seine Komponenten
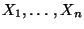 sind genau dann unabhängige Zufallsvariable, wenn
sind genau dann unabhängige Zufallsvariable, wenn




Next: Beispiele
Up: Stochastische Unabhängigkeit
Previous: Unabhängige Ereignisse
Contents
Roland Maier
2001-08-20
![]() unabhängig, wenn die
Ereignisse
unabhängig, wenn die
Ereignisse
![]() und
und
![]() für beliebige
für beliebige
![]() unabhängig im Sinne von Definition 3.16 sind.
unabhängig im Sinne von Definition 3.16 sind.