Next: Funktionen von Zufallsvariablen
Up: Stochastische Unabhängigkeit
Previous: Unabhängige Zufallsvariable
Contents
Beispiele
 -maliger Münzwurf
-maliger Münzwurf
- Betrachten den in Abschnitt 3.2.1 eingeführten
Wahrscheinlichkeitsraum
 mit der Grundmenge
und dem Wahrscheinlichkeitsmaß
mit der Grundmenge
und dem Wahrscheinlichkeitsmaß  , das durch
, das durch
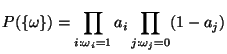 |
(22) |
gegeben ist, wobei
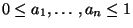 .
.
- Betrachten die Zufallsvariablen
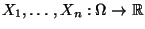 , die gegeben seien durch die
Projektion
, die gegeben seien durch die
Projektion
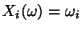 für
für
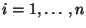 .
.
- Aus (21) und (22) folgt unmittelbar,
daß
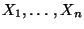 unabhängige Zufallsvariable sind.
unabhängige Zufallsvariable sind.
- Man kann jedoch auch in diesem Modell Zufallsvariablen
konstruieren, die nicht unabhängig sind. Sei nämlich
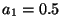 , und sei
, und sei
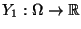 gegeben durch
gegeben durch
- Dann sind
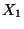 und
und 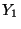 nicht unabhängig, denn es gilt
nicht unabhängig, denn es gilt
- zweidimensionale Normalverteilung
- Betrachten zwei unabhängige Zufallsvariable
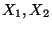 , die standardnormalverteilt sind. D.h.,
, die standardnormalverteilt sind. D.h.,
- Für die (gemeinsame) Dichte
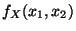 des
Zufallsvektors
des
Zufallsvektors
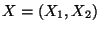 gilt
gilt
- Man sagt dann, daß auch der Zufallsvektor
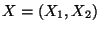 standardnormalverteilt ist.
standardnormalverteilt ist.
- Verallgemeinerung:
Sei
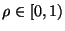 , und sei
, und sei
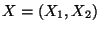 ein absolutstetiger
Zufallsvektor mit der Dichte
ein absolutstetiger
Zufallsvektor mit der Dichte
- Dann gilt für die (Rand-)Dichte
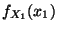 von
von
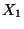
- Durch die Substitution
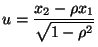
bzw.
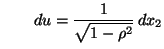
ergibt sich also
- Analog gilt
- Die Komponenten
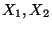 des Zufallsvektors
des Zufallsvektors
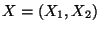 sind also für jedes
sind also für jedes
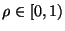 standardnormalverteilt.
standardnormalverteilt.
- Beachte jedoch, daß
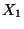 und
und 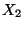 nur dann unabhängig sind,
wenn
nur dann unabhängig sind,
wenn 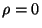 . Denn für
. Denn für 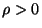 gilt
gilt




Next: Funktionen von Zufallsvariablen
Up: Stochastische Unabhängigkeit
Previous: Unabhängige Zufallsvariable
Contents
Roland Maier
2001-08-20
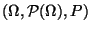 mit der Grundmenge
und dem Wahrscheinlichkeitsmaß
mit der Grundmenge
und dem Wahrscheinlichkeitsmaß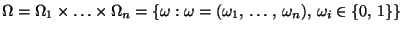
 , das durch
, das durch
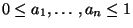 .
.
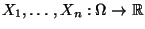 , die gegeben seien durch die
Projektion
, die gegeben seien durch die
Projektion
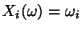 für
für
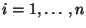 .
.
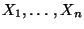 unabhängige Zufallsvariable sind.
unabhängige Zufallsvariable sind.
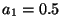 , und sei
, und sei
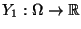 gegeben durch
gegeben durch
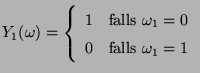
 und
und  nicht unabhängig, denn es gilt
nicht unabhängig, denn es gilt
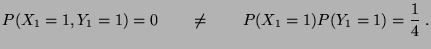
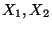 , die standardnormalverteilt sind. D.h.,
, die standardnormalverteilt sind. D.h.,
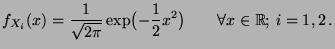
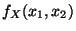 des
Zufallsvektors
des
Zufallsvektors
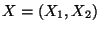 gilt
gilt
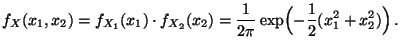
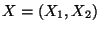 standardnormalverteilt ist.
standardnormalverteilt ist.
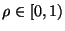 , und sei
, und sei
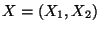 ein absolutstetiger
Zufallsvektor mit der Dichte
ein absolutstetiger
Zufallsvektor mit der Dichte
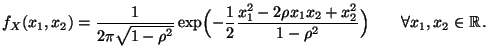
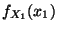 von
von
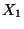
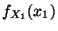

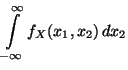

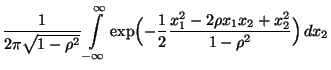
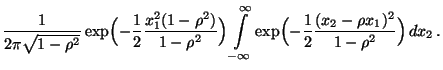
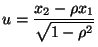 bzw.
bzw.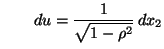
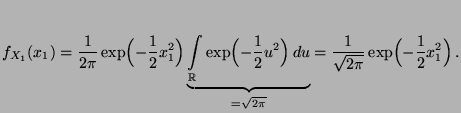
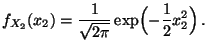
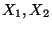 des Zufallsvektors
des Zufallsvektors
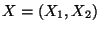 sind also für jedes
sind also für jedes
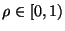 standardnormalverteilt.
standardnormalverteilt.
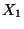 und
und 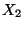 nur dann unabhängig sind,
wenn
nur dann unabhängig sind,
wenn 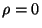 . Denn für
. Denn für 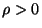 gilt
gilt