Next: Lineare Transformation
Up: Funktionen von Zufallsvariablen
Previous: Funktionen von Zufallsvariablen
Contents
Zusammengesetzte Abbildungen
- Beispiel
 (Klassifikation)
(Klassifikation)
- Manchmal ist es zweckmäßig, die Werte von Zufallsvariablen
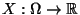 zu klassifizieren. Dabei wird der Wertebereich
zu klassifizieren. Dabei wird der Wertebereich
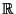 von
von  in
in 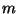 Klassen zerlegt, die wir mit der Menge der
ersten
Klassen zerlegt, die wir mit der Menge der
ersten 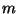 natürlichen Zahlen
natürlichen Zahlen
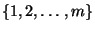 identifizieren.
identifizieren.
- Mit anderen Worten: Außer der Zufallsvariablen
 betrachten wir
noch eine weitere Abbildung
betrachten wir
noch eine weitere Abbildung
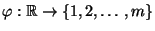 .
.
- Durch Nacheinanderausführung der Abbildungen
 und
und 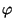 ergibt sich dann die Abbildung
ergibt sich dann die Abbildung
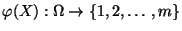 mit
mit
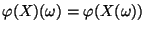 , die jedem
, die jedem
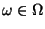 die Klasse
die Klasse
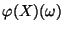 zuordnet.
zuordnet.
- Um die Wahrscheinlichkeit bestimmen zu können, daß die
Zufallsvariable
 Werte in Klasse
Werte in Klasse 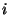 annimmt, muß gewährleistet sein, daß
annimmt, muß gewährleistet sein, daß
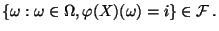 |
(23) |
- Die Abbildung
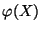 muß also die
Regularitätseigenschaft einer Zufallsvariablen besitzen, d.h. der
Meßbarkeitsbedingung (1) genügen.
muß also die
Regularitätseigenschaft einer Zufallsvariablen besitzen, d.h. der
Meßbarkeitsbedingung (1) genügen.
- Um dies zu erreichen, wird über die
Abbildung
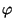 vorausgesetzt, daß
vorausgesetzt, daß
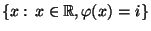 eine Teilmenge von
eine Teilmenge von
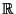 aus
aus
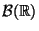 , d.h.
eine Borel-Menge ist, für jedes
, d.h.
eine Borel-Menge ist, für jedes
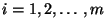 .
.
- Man kann zeigen, daß dann (23) für jedes
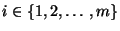 bzw.
bzw.
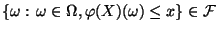 für jedes
für jedes
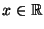 gilt, d.h.,
gilt, d.h.,
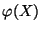 ist eine
Zufallsvariable.
ist eine
Zufallsvariable.
- Beachte
-
Allgemein gilt für zusammengesetzte Abbildungen
- Lemma 3.19
 Sei
Sei
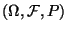 ein beliebiger
Wahrscheinlichkeitsraum, und
ein beliebiger
Wahrscheinlichkeitsraum, und
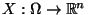 sei ein
beliebiger Zufallsvektor. Falls
sei ein
beliebiger Zufallsvektor. Falls
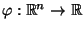 eine
Borel-meßbare Abbildung ist, d.h., falls die Bedingung
(24) erfüllt ist, dann ist die zusammengesetzte Abbildung
eine
Borel-meßbare Abbildung ist, d.h., falls die Bedingung
(24) erfüllt ist, dann ist die zusammengesetzte Abbildung
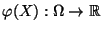 mit
mit
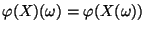 eine (rellwertige)
Zufallsvariable, d.h., es gilt
eine (rellwertige)
Zufallsvariable, d.h., es gilt
- Beispiel
-
- Beachte
-




Next: Lineare Transformation
Up: Funktionen von Zufallsvariablen
Previous: Funktionen von Zufallsvariablen
Contents
Roland Maier
2001-08-20
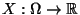 zu klassifizieren. Dabei wird der Wertebereich
zu klassifizieren. Dabei wird der Wertebereich
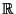 von
von  in
in 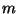 Klassen zerlegt, die wir mit der Menge der
ersten
Klassen zerlegt, die wir mit der Menge der
ersten 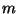 natürlichen Zahlen
natürlichen Zahlen
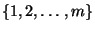 identifizieren.
identifizieren.
 betrachten wir
noch eine weitere Abbildung
betrachten wir
noch eine weitere Abbildung
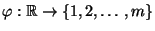 .
.
 und
und 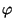 ergibt sich dann die Abbildung
ergibt sich dann die Abbildung
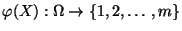 mit
mit
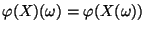 , die jedem
, die jedem
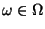 die Klasse
die Klasse
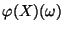 zuordnet.
zuordnet.
 Werte in Klasse
Werte in Klasse 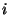 annimmt, muß gewährleistet sein, daß
annimmt, muß gewährleistet sein, daß
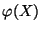 muß also die
Regularitätseigenschaft einer Zufallsvariablen besitzen, d.h. der
Meßbarkeitsbedingung (1) genügen.
muß also die
Regularitätseigenschaft einer Zufallsvariablen besitzen, d.h. der
Meßbarkeitsbedingung (1) genügen.
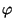 vorausgesetzt, daß
vorausgesetzt, daß
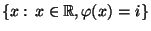 eine Teilmenge von
eine Teilmenge von
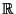 aus
aus
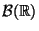 , d.h.
eine Borel-Menge ist, für jedes
, d.h.
eine Borel-Menge ist, für jedes
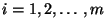 .
.
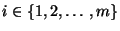 bzw.
bzw.
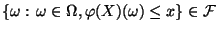 für jedes
für jedes
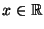 gilt, d.h.,
gilt, d.h.,
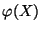 ist eine
Zufallsvariable.
ist eine
Zufallsvariable.
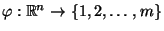 von Zufallsvektoren
von Zufallsvektoren
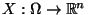 .
.
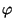 formuliert
werden kann, so daß die zusammengesetzte Abbildung
formuliert
werden kann, so daß die zusammengesetzte Abbildung
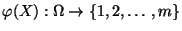 eine
Zufallsvariable ist, wird die Borel-
eine
Zufallsvariable ist, wird die Borel-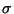 -Algebra
-Algebra
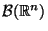 von Teilmengen des
von Teilmengen des
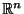 betrachtet.
betrachtet.
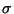 -Algebra
von Teilmengen des
-Algebra
von Teilmengen des
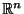 , die alle offenen Quader
, die alle offenen Quader
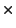
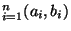 enthält;
enthält;
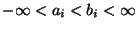 . D.h.
. D.h.
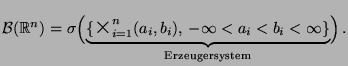
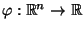 heißt Borel-meßbar, wenn
heißt Borel-meßbar, wenn