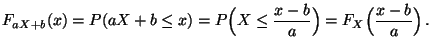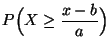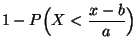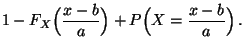Next: Quadrierung
Up: Funktionen von Zufallsvariablen
Previous: Zusammengesetzte Abbildungen
Contents
Lineare Transformation
Ein wichtiger Spezialfall einer zusammengesetzten Abbildung ist
die lineare Transformation von Zufallsvariablen, wobei 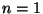 und
und
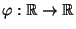 mit
mit
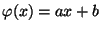 ;
;
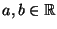 .
.
- Theorem 3.20
 Sei
Sei
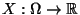 eine beliebige Zufallsvariable und
eine beliebige Zufallsvariable und
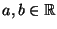 beliebige Zahlen mit
beliebige Zahlen mit 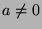 . Dann ist
. Dann ist 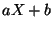 eine Zufallsvariable,
und
eine Zufallsvariable,
und
- die Verteilungsfunktion von
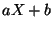 ist
gegeben durch
ist
gegeben durch
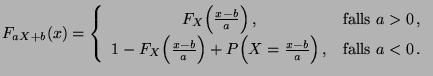 |
(27) |
- falls
 absolutstetig ist mit der Dichte
absolutstetig ist mit der Dichte 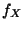 , dann ist auch
, dann ist auch
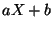 absolutstetig mit der Dichte
absolutstetig mit der Dichte
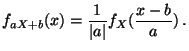 |
(28) |
- Beweis
 Falls
Falls 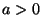 , dann gilt
Analog ergibt sich für
, dann gilt
Analog ergibt sich für 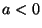
Damit ist (27) bewiesen. Sei nun  absolutstetig. Falls
die Dichte
absolutstetig. Falls
die Dichte 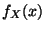 von
von  eine stetige Funktion ist, dann ergibt
sich (28) durch beidseitiges Differenzieren von
(27). Ansonsten nutzt man die Tatsache, daß zwischen
Verteilungsfunktion und Dichte einer Zufallsvariablen eine
eineindeutige Zuordnung besteht, und zeigt, daß das Integral von
eine stetige Funktion ist, dann ergibt
sich (28) durch beidseitiges Differenzieren von
(27). Ansonsten nutzt man die Tatsache, daß zwischen
Verteilungsfunktion und Dichte einer Zufallsvariablen eine
eineindeutige Zuordnung besteht, und zeigt, daß das Integral von
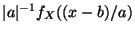 die Verteilungsfunktion von
die Verteilungsfunktion von 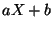 ergibt.
ergibt.
- Beispiel
-




Next: Quadrierung
Up: Funktionen von Zufallsvariablen
Previous: Zusammengesetzte Abbildungen
Contents
Roland Maier
2001-08-20
![]() und
und
![]() mit
mit
![]() ;
;
![]() .
.