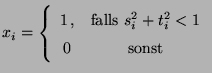Next: Zentraler Grenzwertsatz
Up: Abschätzungen und Grenzwertsätze
Previous: Gesetz der großen Zahlen
Contents
Beispiel (Buffonsches
Nadelexperiment)
(Buffonsches
Nadelexperiment)
- Das Buffonsche Nadelexperiment ist ein Beispiel, bei dem das
starke Gesetz der großen Zahlen angewendet wird.
- Es ist eine der ersten numerischen
Methoden, die auf stochastischen Gesetzmäßigkeiten beruht.
- Der ,,Erfinder'' ist
Georges Louis Leclerc Comte de Buffon (1707-1788).
- Heute sind solche Verfahren unter der Bezeichnung
,,Monte-Carlo-Simulation'' bekannt.
- Betrachten das System
von parallelen und äquidistanten (vertikalen) Geraden
in der euklidischen Ebene
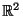 .
.
- Werfen eine Nadel mit der Länge 1
,,willkürlich'' in die Ebene
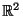 , wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
, wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
- Betrachten zwei Zufallsvariable
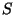 und
und 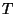 ,
die die zufällige Lage der Nadel beschreiben, wobei
,
die die zufällige Lage der Nadel beschreiben, wobei
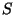 der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von
der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von 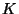 ist,
ist,
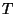 der Winkel ist, den die Nadel zum Lot auf die
Geraden von
der Winkel ist, den die Nadel zum Lot auf die
Geraden von 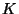 bildet, und
bildet, und
- die Zufallsvariablen
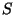 und
und 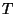 unabhängig und gleichverteilt seien auf den Intervallen
unabhängig und gleichverteilt seien auf den Intervallen
![$ [0,1]$](img1069.png) bzw.
bzw.
![$ [-\pi/2,\pi/2]$](img1070.png) .
.
- Bestimmen die Wahrscheinlichkeit des
Ereignisses
daß die willkürlich geworfene Nadel eine der Geraden
von
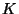 schneidet.
schneidet.
- Es gilt
- Aus der Gleichung
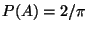 ergibt sich nun eine Methode zur
experimentellen Bestimmung der Zahl
ergibt sich nun eine Methode zur
experimentellen Bestimmung der Zahl 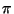 , die auf dem Gesetz der
großen Zahlen beruht.
, die auf dem Gesetz der
großen Zahlen beruht.
- Seien
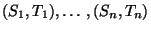 unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie
unabhängige und
identisch verteilte Zufallsvektoren (mit der gleichen
Verteilung wie 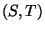 ), die wir als
das Ergebnis von
), die wir als
das Ergebnis von  (unabhängig durchgeführten) Nadelexperimenten auffassen.
(unabhängig durchgeführten) Nadelexperimenten auffassen.
- Dann sind
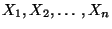 mit
unabhängige und identisch verteilte Zufallsvariable
mit dem Erwartungswert
mit
unabhängige und identisch verteilte Zufallsvariable
mit dem Erwartungswert
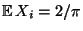 .
.
- Aus Theorem 4.22 ergibt sich also, daß das
arithmetische Mittel
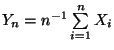 fast sicher gegen die Zahl
fast sicher gegen die Zahl 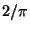 strebt.
strebt.
- D.h., für große
 ist
ist 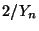 mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
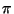 .
.
- Beachte
 Im Internet gibt es zahlreiche Seiten, wo dieses Verfahren
implementiert worden ist und mittels JAVA-Applets
auch selbst durchgeführt werden kann, vgl. beispielsweise
Im Internet gibt es zahlreiche Seiten, wo dieses Verfahren
implementiert worden ist und mittels JAVA-Applets
auch selbst durchgeführt werden kann, vgl. beispielsweise
Ein anderer Algorithmus zur experimentellen
Bestimmung der Zahl 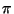 hängt ebenfalls mit einem einfachen
geometrischen Sachverhalt zusammen.
hängt ebenfalls mit einem einfachen
geometrischen Sachverhalt zusammen.
- Beachte
-
- Bei der Implementierung dieser Monte-Carlo-Simulation
kann man wie folgt vorgehen.
- Ein JAVA-Applet, mit dem dieses Simulationsverfahren
selbst durchgeführt werden kann, findet man beispielsweise
auf der Internet-Seite:




Next: Zentraler Grenzwertsatz
Up: Abschätzungen und Grenzwertsätze
Previous: Gesetz der großen Zahlen
Contents
Roland Maier
2001-08-20
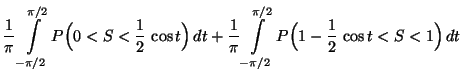
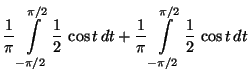
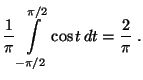
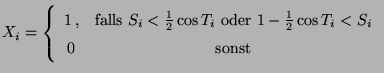
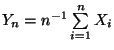 fast sicher gegen die Zahl
fast sicher gegen die Zahl ![]() hängt ebenfalls mit einem einfachen
geometrischen Sachverhalt zusammen.
hängt ebenfalls mit einem einfachen
geometrischen Sachverhalt zusammen.
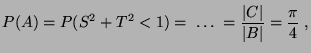
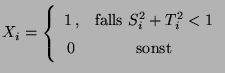
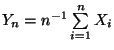 fast sicher gegen die Zahl
fast sicher gegen die Zahl