



Next: Beispiel (Buffonsches Nadelexperiment)
Up: Abschätzungen und Grenzwertsätze
Previous: Tschebyschewsche Ungleichung
Contents
Gesetz der großen Zahlen
Wir diskutieren nun zwei allgemeinere Varianten des Gesetzes der
großen Zahlen, das bereits in Abschnitt 4.1.1 im
Zusammenhang mit dem Beispiel des wiederholten Würfelns erwähnt
wurde. Dabei
Aus der Tschebyschewschen Ungleichung (40) ergibt sich
- Theorem 4.20
 Sei
Sei
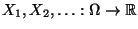 eine Folge von Zufallsvariablen mit dem
gleichen Erwartungswert
eine Folge von Zufallsvariablen mit dem
gleichen Erwartungswert
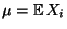 und
mit
und
mit
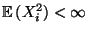 für alle
für alle
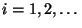 .
.
- Falls
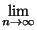 Var Var 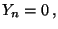 |
(45) |
dann gilt für jedes
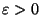
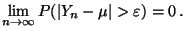 |
(46) |
- Die Bedingung (45) ist insbesondere
dann erfüllt, wenn die Zufallsvariablen
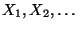 unabhängig sind mit der gleichen
Varianz
unabhängig sind mit der gleichen
Varianz
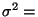 Var
Var  für alle
für alle
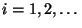 .
.
- Beweis
-
- Definition 4.21
 Man sagt, daß die Zufallsvariablen
Man sagt, daß die Zufallsvariablen
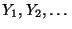 stochastisch
gegen die Zahl
stochastisch
gegen die Zahl
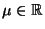 konvergieren, falls
(46) für jedes
konvergieren, falls
(46) für jedes
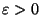 gilt.
gilt. Schreibweise:
Schreibweise:
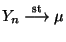
- Beachte
-
- Die stochastische Konvergenz wird auch
Konvergenz in Wahrscheinlichkeit genannt.
- Die Konvergenz (46) des arithmetischen
Mittels
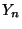 gegen den Erwartungswert
gegen den Erwartungswert 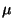 heißt das
schwache Gesetz der großen Zahlen.
heißt das
schwache Gesetz der großen Zahlen.
Neben der stochastischen Konvergenz gibt es noch weitere
Konvergenzarten von Zufallsvariablen. Insbesondere gilt neben
Theorem 4.20 der folgende Grenzwertsatz.
- Theorem 4.22
 Sei
Sei
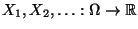 eine Folge von unabhängigen und identisch verteilten
Zufallsvariablen mit
eine Folge von unabhängigen und identisch verteilten
Zufallsvariablen mit
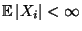 für alle
für alle
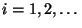 ;
;
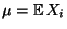 . Für das arithmetische Mittel
. Für das arithmetische Mittel
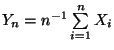 gilt dann
gilt dann
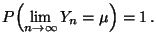 |
(47) |
- Beweis
 Der Beweis von Theorem 4.22 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
Der Beweis von Theorem 4.22 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
- Definition 4.23
 Man sagt, daß die Zufallsvariablen
Man sagt, daß die Zufallsvariablen
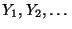 fast sicher
gegen die Zahl
fast sicher
gegen die Zahl
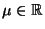 konvergieren, falls
(47) gilt.
konvergieren, falls
(47) gilt. Schreibweise:
Schreibweise:
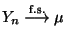
- Beachte
-
- Die fast sichere Konvergenz wird auch
Konvergenz mit Wahrscheinlichkeit 1 genannt.
- Man kann zeigen, daß die fast sichere Konvergenz
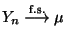 einer Folge von Zufallsvariablen
einer Folge von Zufallsvariablen
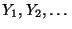 stets die stochastische Konvergenz
stets die stochastische Konvergenz
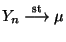 impliziert.
impliziert.
- Die Konvergenz (47) des arithmetischen
Mittels
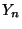 gegen den Erwartungswert
gegen den Erwartungswert 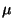 heißt
deshalb das starke Gesetz der großen Zahlen.
heißt
deshalb das starke Gesetz der großen Zahlen.
- Schließlich sei noch erwähnt, daß man in Theorem 4.22
(analog zur Situation in Theorem 4.20) die Bedingungen
der Unabhängigkeit bzw. der identischen Verteiltheit der
Zufallsvariablen
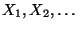 durch schwächere
Bedingungen ersetzen kann, ohne daß dabei die
Gültigkeit von (47) verloren geht.
durch schwächere
Bedingungen ersetzen kann, ohne daß dabei die
Gültigkeit von (47) verloren geht.




Next: Beispiel (Buffonsches Nadelexperiment)
Up: Abschätzungen und Grenzwertsätze
Previous: Tschebyschewsche Ungleichung
Contents
Roland Maier
2001-08-20
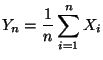
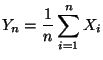
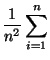 Var
Var 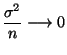
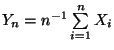 gilt dann
gilt dann