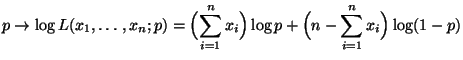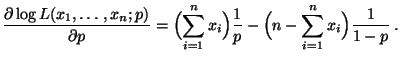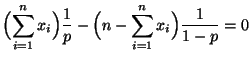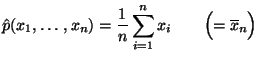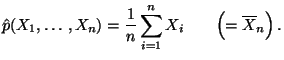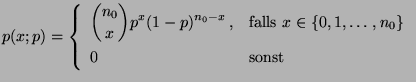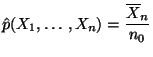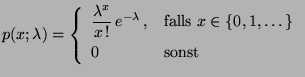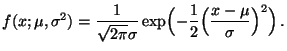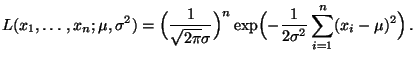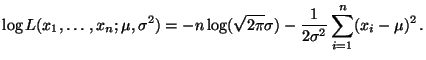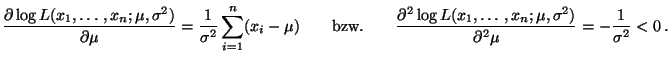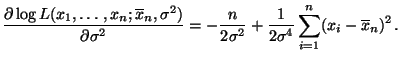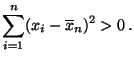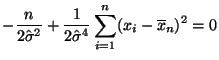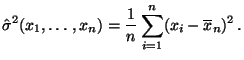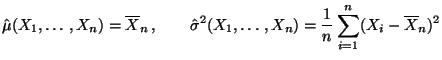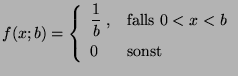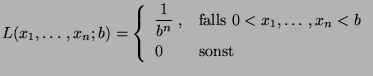Next: Konfidenzintervalle
Up: Schätzung von Parametern
Previous: Momentenmethode
Contents
Maximum-Likelihood-Methode
- Eine andere Methode zur Gewinnung von Schätzern für die
unbekannten Komponenten des Parametervektors
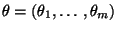 ist die
Maximum-Likelihood-Methode.
ist die
Maximum-Likelihood-Methode.
- Genauso wie bei der Momentenmethode wird auch bei der
Maximum-Likelihood-Methode das Ziel verfolgt,
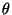 so zu
schätzen, daß eine möglichst gute Anpassung der
Modellcharakteristiken
so zu
schätzen, daß eine möglichst gute Anpassung der
Modellcharakteristiken 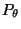 bzw.
bzw. 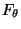 an die
beobachteten Daten erreicht wird.
an die
beobachteten Daten erreicht wird.
- Dabei wird bei der Maximum-Likelihood-Methode die
Wahrscheinlichkeit für das Eintreten bestimmter (infinitesimaler)
Ereignisse maximiert.
- Als der ,,Erfinder'' der Maximum-Likelihood-Methode gilt Sir
Ronald Aylmer Fisher (1890-1962).
Wir betrachten nur die beiden (grundlegenden) Fälle, daß die
Stichprobenvariablen
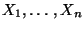 entweder diskret oder
absolutstetig sind. D.h., für jedes
entweder diskret oder
absolutstetig sind. D.h., für jedes
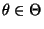 gelte
entweder
gelte
entweder
-
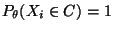 für eine abzählbare Menge
für eine abzählbare Menge
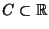 ,
,
- wobei wir mit
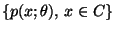 die
Wahrscheinlichkeitsfunktion von
die
Wahrscheinlichkeitsfunktion von 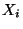 bezeichnen;
bezeichnen;
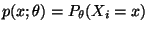
oder
-
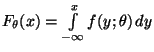 für jedes
für jedes
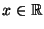 ,
,
- wobei
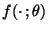 die Dichte von
die Dichte von 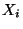 ist.
ist.
- Definition 5.18
 Die Abbildung
Die Abbildung
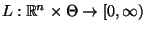 sei durch die folgende
Vorschrift gegeben.
sei durch die folgende
Vorschrift gegeben.
- Falls
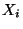 diskret ist, dann gelte
diskret ist, dann gelte
 |
(33) |
- Falls
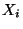 absolutstetig ist, dann gelte
absolutstetig ist, dann gelte
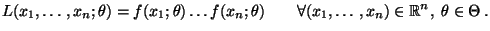 |
(34) |
Für jeden Vektor
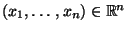 heißt die Abbildung
heißt die Abbildung
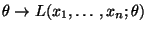 die Likelihood-Funktion
der Stichprobe
die Likelihood-Funktion
der Stichprobe
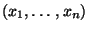 .
.
Die Idee der Maximum-Likelihood-Methode besteht nun darin, für
jede (konkrete) Stichprobe
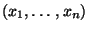 einen
Parametervektor
einen
Parametervektor
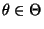 zu bestimmen, so daß der Wert
zu bestimmen, so daß der Wert
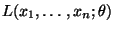 der Likelihood-Funktion möglichst groß
wird. Dies führt zu der folgenden
der Likelihood-Funktion möglichst groß
wird. Dies führt zu der folgenden
- Definition 5.19
 Sei
Sei
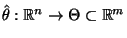 eine Stichprobenfunktion
mit
eine Stichprobenfunktion
mit
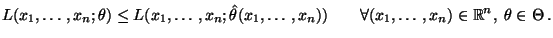 |
(35) |
Der Zufallsvektor
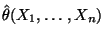 wird dann Maximum-Likelihood-Schätzer von
wird dann Maximum-Likelihood-Schätzer von 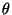 genannt.
genannt.
- Beispiel
-
- Beachte
-
- Beispiele
-
- Bernoulli-Verteilung
- Betrachten die Familie
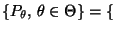 Bin
Bin
![$ (1,p),\,p\in[0,1]\}$](img1342.png) der Bernoulli-Verteilungen.
der Bernoulli-Verteilungen.
- Dann gilt
- Die Likelihood-Funktion
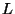 ist also gegeben durch
ist also gegeben durch
- Falls
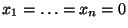 bzw.
bzw.
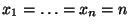 , dann
sieht man leicht, daß
die Abbildung
, dann
sieht man leicht, daß
die Abbildung
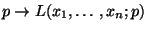 an der Stelle
an der Stelle 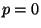 bzw.
bzw. 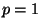 ein
(eindeutig bestimmtes) Maximum hat.
ein
(eindeutig bestimmtes) Maximum hat.
- Sei nun
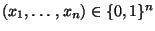 mit
mit
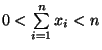 . Dann ist
eine stetige Funktion im Intervall
. Dann ist
eine stetige Funktion im Intervall 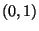 , und es gilt
, und es gilt

bzw.
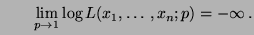
- Die Abbildung
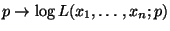 hat also ein Maximum im
Intervall
hat also ein Maximum im
Intervall 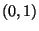 .
.
- Durch Differenzieren nach
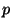 ergibt sich
ergibt sich
- Weil die Gleichung
die (eindeutig bestimmte) Lösung
hat, nimmt die Abbildung
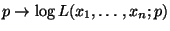 an der Stelle
an der Stelle
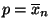 ihr Maximum an.
ihr Maximum an.
- Also ist der Maximum-Likelihood-Schätzer für den Parameter
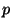 gegeben durch
gegeben durch
- Binomial-Verteilung
- Für eine beliebige, jedoch vorgegebene
(d.h. bekannte) natürliche Zahl
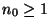 betrachten wir nun
die Familie
betrachten wir nun
die Familie
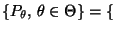 Bin
Bin
![$ (n_0,p),\,p\in[0,1]\}$](img1362.png) von Binomialerteilungen.
von Binomialerteilungen.
- Dann gilt
- Genauso wie in Beispiel 1 ergibt sich der
Maximum-Likelihood-Schätzer
für den (unbekannten) Parameter
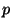 .
.
- Poisson-Verteilung
- Betrachten die Familie
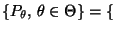 Poi
Poi
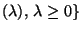 der Poisson-Verteilungen.
der Poisson-Verteilungen.
- Dann gilt
- Auf die gleiche Weise wie in den Beispielen 1 und 2 ergibt sich der
Maximum-Likelihood-Schätzer
für den Parameter
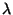 .
.
- Normalverteilung
- Betrachten nun die Familie
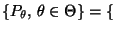 N
N
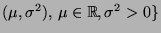 der Normalverteilungen.
der Normalverteilungen.
- Dann gilt
- Die Likelihood-Funktion
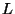 ist somit gegeben durch
ist somit gegeben durch
- Für die Loglikelihood-Funktion gilt
- Durch Differenzieren nach
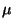 ergibt sich
ergibt sich
- Für jedes (fest vorgegebene)
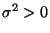 nimmt also die
Abbildung
ihr Maximum an der Stelle
nimmt also die
Abbildung
ihr Maximum an der Stelle
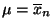 an.
an.
- Es ist nun noch das Maximum der Abbildung
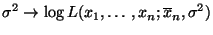 |
(37) |
zu bestimmen.
- Weil
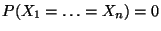 gilt, können wir annehmen, daß
nicht alle Stichprobenwerte
gilt, können wir annehmen, daß
nicht alle Stichprobenwerte
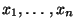 gleich sind.
gleich sind.
- Dann ist die Abbildung (37) stetig für alle
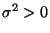 ,
und es gilt
,
und es gilt
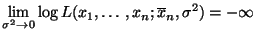
bzw.
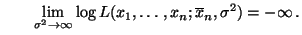
- Die Abbildung (37) hat also ein Maximum im
Intervall
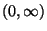 .
.
- Durch Differenzieren nach
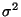 ergibt sich
ergibt sich
- Weil vorausgesetzt wird, daß nicht alle Stichprobenwerte
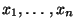 gleich sind, gilt
gleich sind, gilt
- Deshalb hat die Gleichung
die (eindeutig bestimmte) Lösung
- Hieraus ergeben sich die Maximum-Likelihood-Schätzer
für die Parameter
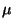 und
und 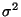 .
.
- Gleichverteilung
- Betrachten die Familie
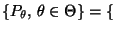 U
U
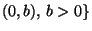 von Gleichverteilungen.
von Gleichverteilungen.
- Dann gilt
- Die Likelihood-Funktion
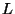 ist somit gegeben durch
ist somit gegeben durch
- Weil die Abbildung
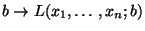 monoton
fallend ist für
monoton
fallend ist für
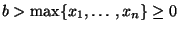 , ergibt
sich der Maximum-Likelihood-Schätzer
, ergibt
sich der Maximum-Likelihood-Schätzer
für den Parameter 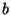 .
.




Next: Konfidenzintervalle
Up: Schätzung von Parametern
Previous: Momentenmethode
Contents
Roland Maier
2001-08-20
![]() entweder diskret oder
absolutstetig sind. D.h., für jedes
entweder diskret oder
absolutstetig sind. D.h., für jedes
![]() gelte
entweder
gelte
entweder
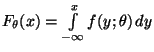 für jedes
für jedes
![]() einen
Parametervektor
einen
Parametervektor
![]() zu bestimmen, so daß der Wert
zu bestimmen, so daß der Wert
![]() der Likelihood-Funktion möglichst groß
wird. Dies führt zu der folgenden
der Likelihood-Funktion möglichst groß
wird. Dies führt zu der folgenden
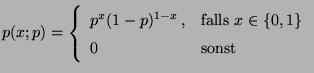
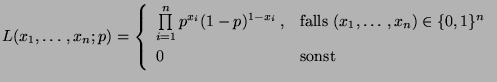
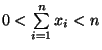 . Dann ist
. Dann ist