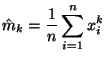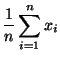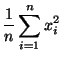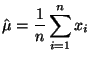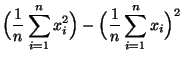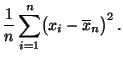Next: Maximum-Likelihood-Methode
Up: Schätzung von Parametern
Previous: Eigenschaften von Parameterschätzern
Contents
Momentenmethode
- Die Momentenmethode ist ein spezielles Verfahren zur Gewinnung von
Schätzern für die unbekannten Komponenten des Parametervektors
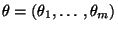 .
.
- Sie beruht auf dem Vergleich von Momenten der Stichprobenvariablen
mit den entsprechenden empirischen Momenten.
Dabei werden die folgenden Modellannahmen gemacht.
Die Momentenmethode besteht aus den folgenden Schritten:
- Für jedes
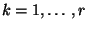 bestimmen wir das
bestimmen wir das 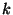 -te empirische Moment
-te empirische Moment
- und lösen das Gleichungssystem
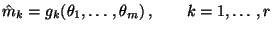 |
(29) |
nach den Unbekannten
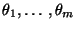 auf.
auf.
Die Lösung von (29) bezeichnen wir mit
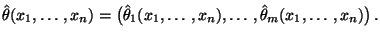 |
(30) |
Dabei wird vorausgesetzt, daß
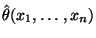 eindeutig bestimmt ist und daß die Abbildung
eindeutig bestimmt ist und daß die Abbildung
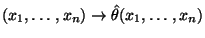
eine Stichprobenfunktion ist, die den Stichprobenraum
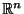 in
den Parameterraum
in
den Parameterraum
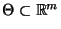 abbildet.
abbildet.
- Definition 5.17
 Der Zufallsvektor
Der Zufallsvektor
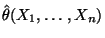 heißt Momentenschätzer des
Parametervektors
heißt Momentenschätzer des
Parametervektors 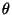 , wobei in (30) die
Zufallsstichprobe
, wobei in (30) die
Zufallsstichprobe
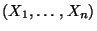 anstelle der konkreten
Stichprobe
anstelle der konkreten
Stichprobe
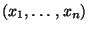 eingesetzt wird.
eingesetzt wird.
- Beachte
-
- Es gibt Beispiele parametrischer Verteilungsfamilien, so daß das
Gleichungssystem (29) für
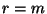 keine eindeutig
bestimmte Lösung besitzt.
keine eindeutig
bestimmte Lösung besitzt.
- Dann ist
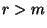 , d.h., die Anzahl der betrachteten Momente kann
größer als die Anzahl der (unbekannten) Parameterkomponenten
sein.
, d.h., die Anzahl der betrachteten Momente kann
größer als die Anzahl der (unbekannten) Parameterkomponenten
sein.
- In vielen Fällen ist jedoch das Gleichungssystem (29)
für
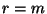 eindeutig lösbar.
eindeutig lösbar.
- Beispiel
 Die Stichprobenvariablen
Die Stichprobenvariablen  seien normalverteilt,
d.h., es gelte (26). Dann ist
seien normalverteilt,
d.h., es gelte (26). Dann ist
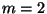 mit
mit
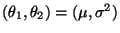
- Außerdem ist
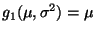
und
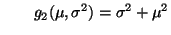
- Das Gleichungssystem (29) hat also die Form
- Durch Umstellen ergibt sich
und
- D.h., bei normalverteilten Stichprobenvariablen
 ergeben sich
mit der Momentenmethode die Schätzer
ergeben sich
mit der Momentenmethode die Schätzer
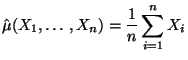 |
(31) |
und
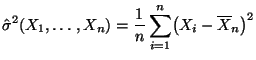 |
(32) |
für die Modellparameter 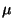 bzw.
bzw. 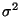 .
.
- Beachte

- Aus den Theoremen 5.4 und 5.5 ergibt sich, daß der in (31)
gewonnene Schätzer
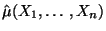 des Parameters
des Parameters 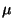 erwartungstreu und konsistent ist.
erwartungstreu und konsistent ist.
- Aus den Theoremen 5.7 und 5.8 ergibt sich, daß der in (32)
gewonnene Schätzer
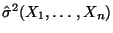 des Parameters
des Parameters 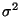 asymptotisch erwartungstreu und konsistent ist.
asymptotisch erwartungstreu und konsistent ist.
- Wegen des im Vergleich zu
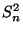 modifizierten
Normierungsfaktors
modifizierten
Normierungsfaktors 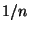 ist
ist
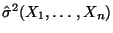 jedoch nicht erwartungstreu.
jedoch nicht erwartungstreu.
- Somit ist auch der Schätzer
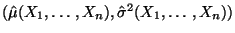 des Parametervektors
des Parametervektors
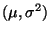 lediglich asymptotisch erwartungstreu und konsistent.
lediglich asymptotisch erwartungstreu und konsistent.




Next: Maximum-Likelihood-Methode
Up: Schätzung von Parametern
Previous: Eigenschaften von Parameterschätzern
Contents
Roland Maier
2001-08-20