



Next: Eigenschaften von Parameterschätzern
Up: Methoden der Statistik
Previous: Empirische Verteilungsfunktion
Contents
Schätzung von Parametern
In diesem Abschnitt setzen wir zusätzlich voraus, daß
- die Verteilungsfunktion
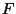 der Stichprobenvariablen
der Stichprobenvariablen  zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
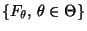 gehört,
gehört,
- wobei die Menge
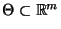 Parameterraum genannt wird
und
Parameterraum genannt wird
und
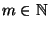 eine beliebige, jedoch vorgegebene natürliche Zahl ist.
eine beliebige, jedoch vorgegebene natürliche Zahl ist.
- Mit anderen Worten: Es gelte
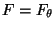 für ein
für ein
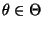 ,
,
- wobei jedoch der Parametervektor
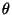 (bzw. ein Teil seiner Komponenten) unbekannt sei
(bzw. ein Teil seiner Komponenten) unbekannt sei
- und aus den beobachteten Daten
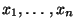 geschätzt
werden soll.
geschätzt
werden soll.
Wir nehmen an, daß der Wahrscheinlichkeitsraum
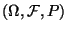 ,
über dem die Stichprobenvariablen
,
über dem die Stichprobenvariablen
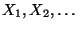 definiert sind,
der sogenannte kanonische Wahrscheinlichkeitsraum ist, vgl.
auch das in Abschnitt 4.1.1 diskutierte Beispiel des
wiederholten Würfelns. Das heißt, daß
definiert sind,
der sogenannte kanonische Wahrscheinlichkeitsraum ist, vgl.
auch das in Abschnitt 4.1.1 diskutierte Beispiel des
wiederholten Würfelns. Das heißt, daß
- Beachte
-
- Das in (25) definierte Wahrscheinlichkeitsmaß
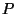 bezeichnen wir im folgenden gelegentlich mit
bezeichnen wir im folgenden gelegentlich mit 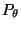 , um zu betonen, daß
, um zu betonen, daß
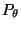 von dem (unbekannten) Parametervektor
von dem (unbekannten) Parametervektor
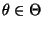 abhängt.
abhängt.
- Entsprechend verwenden wir die Bezeichnungen
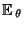 und
Var
und
Var 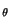 für Erwartungswert bzw. Varianz.
für Erwartungswert bzw. Varianz.
- Falls keine Verwechslung möglich ist, dann bezeichnen wir
auch die Verteilung einer (einzelnen) Stichprobenvariablen
 mit
mit 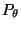 , d.h.
, d.h.
![$ P_\theta(X_i\le
x_i)=P_\theta((-\infty,x_i])=F_\theta(x_i)$](img1240.png) .
.
- Beispiel
 Die wichtigste parametrische Familie
Die wichtigste parametrische Familie
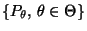 von
Verteilungen, die in diesem Abschnitt betrachtet wird, ist die Normalverteilungsfamilie
von
Verteilungen, die in diesem Abschnitt betrachtet wird, ist die Normalverteilungsfamilie
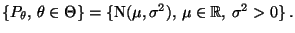 |
(26) |
In diesem Fall ist 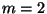 ,
,
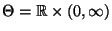 und
und
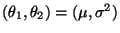 .
.
- Beachte
 Weitere Beispiele von Familien parametrischer Verteilungen, die im
bisherigen Verlauf der Vorlesung betrachtet wurden, sind die
Weitere Beispiele von Familien parametrischer Verteilungen, die im
bisherigen Verlauf der Vorlesung betrachtet wurden, sind die
- hypergeometrische Verteilung,
- Binomialverteilung,
- Poisson-Verteilung,
- Exponentialverteilung,
- (diskrete bzw. stetige) Gleichverteilung.
Subsections




Next: Eigenschaften von Parameterschätzern
Up: Methoden der Statistik
Previous: Empirische Verteilungsfunktion
Contents
Roland Maier
2001-08-20
![]() ,
über dem die Stichprobenvariablen
,
über dem die Stichprobenvariablen
![]() definiert sind,
der sogenannte kanonische Wahrscheinlichkeitsraum ist, vgl.
auch das in Abschnitt 4.1.1 diskutierte Beispiel des
wiederholten Würfelns. Das heißt, daß
definiert sind,
der sogenannte kanonische Wahrscheinlichkeitsraum ist, vgl.
auch das in Abschnitt 4.1.1 diskutierte Beispiel des
wiederholten Würfelns. Das heißt, daß