



Next: Konfidenzintervalle bei Normalverteilung; Quantilfunktion
Up: Konfidenzintervalle
Previous: Konfidenzintervalle
Contents
Modellbeschreibung
In diesem Abschnitt setzen wir (so wie in Abschnitt 5.2)
voraus, daß
- die Verteilungsfunktion
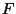 der Stichprobenvariablen
der Stichprobenvariablen  zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
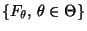 gehört;
gehört;
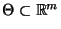 .
.
Dabei nehmen wir (zur Vereinfachnug der Darlegungen) an, daß
- jeweils nur eine einzelne Komponente
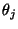 des Parametervektors
des Parametervektors
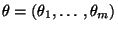 aus den beobachteten Daten
aus den beobachteten Daten
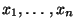 geschätzt werden soll;
geschätzt werden soll;
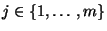 .
.
Genauso wie in Abschnitt 5.2 nehmen wir an, daß
- der Wahrscheinlichkeitsraum
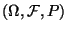 , über dem die
Stichprobenvariablen
, über dem die
Stichprobenvariablen
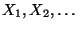 definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvariablen
ist.
definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvariablen
ist.
Anstelle eine (einzelne) Stichprobenfunktion zu betrachten, wie
wir es in den Abschnitten 5.1 und 5.2 tun,
betrachten wir nun
- zwei Stichprobenfunktionen
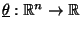 und
und
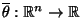 , so daß
, so daß
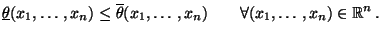 |
(38) |
- Definition 5.20
 Sei
Sei
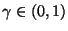 eine beliebige,
jedoch fest vorgegebene Zahl. Dann heißt das zufällige Intervall
eine beliebige,
jedoch fest vorgegebene Zahl. Dann heißt das zufällige Intervall
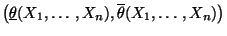 Konfidenzintervall für
Konfidenzintervall für 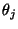 zum Niveau
zum Niveau 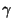 ,
falls
,
falls
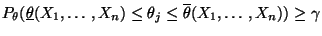 |
(39) |
für jedes
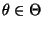 .
.
- Beachte
-
Die praktische Berechnung eines (konkreten)
Konfidenzintervalls
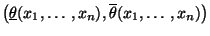 für
für 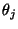 auf der Basis einer (konkreten) Stichprobe
auf der Basis einer (konkreten) Stichprobe
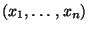 besteht aus den folgenden Schritten:
besteht aus den folgenden Schritten:
- Bestimmen zwei Stichprobenfunktionen
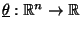 und
und
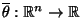 , so daß
, so daß
- (38) gilt und
- eine der Bedingungen (39)-(41)
erfüllt ist.
- Berechnen die Funktionswerte
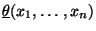 und
und
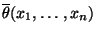 .
.




Next: Konfidenzintervalle bei Normalverteilung; Quantilfunktion
Up: Konfidenzintervalle
Previous: Konfidenzintervalle
Contents
Roland Maier
2001-08-20
![]() für
für ![]() auf der Basis einer (konkreten) Stichprobe
auf der Basis einer (konkreten) Stichprobe
![]() besteht aus den folgenden Schritten:
besteht aus den folgenden Schritten: