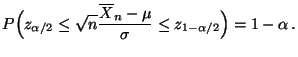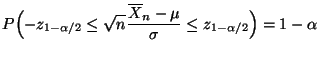Next: Statistische Prüfverteilungen
Up: Konfidenzintervalle
Previous: Modellbeschreibung
Contents
Konfidenzintervalle bei Normalverteilung;
Quantilfunktion
In diesem Abschnitt nehmen wir an, daß die Stichprobenvariablen
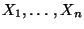 normalverteilt sind, d.h., es gelte
normalverteilt sind, d.h., es gelte
Dabei benötigen wir die folgende
- Definition 5.21
-
- Beachte
-
- Wenn
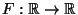 eine beliebige monoton wachsende rechtsstetige
Funktion ist (die nicht unbedingt eine Verteilungsfunktion sein
muß), dann heißt die in (42) definierte Funktion
eine beliebige monoton wachsende rechtsstetige
Funktion ist (die nicht unbedingt eine Verteilungsfunktion sein
muß), dann heißt die in (42) definierte Funktion
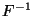 verallgemeinerte inverse Funktion von
verallgemeinerte inverse Funktion von 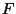 .
.
- Quantilfunktionen sind also spezielle verallgemeinerte inverse
Funktionen.
Bei der Bestimmung von Konfidenzintervallen für normalverteilte
Stichprobenvariablen wird insbesondere die Quantilfunktion der
Standardnormalverteilung benötigt.
- Beachte
-
- Beispiel
 Konfidenzintervall für den Erwartungswert
Konfidenzintervall für den Erwartungswert 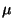 (bei
bekannter Varianz
(bei
bekannter Varianz 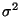 )
)
- Wir nehmen an, daß
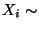 N
N
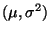 für ein
(unbekanntes)
für ein
(unbekanntes)
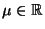 und ein (bekanntes)
und ein (bekanntes)
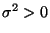 .
.
- Man kann leicht zeigen, daß
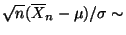 N
N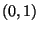 , vgl. das Beispiel in
Abschnitt 3.6.2 bzw. den Kommentar nach Theorem 3.22.
, vgl. das Beispiel in
Abschnitt 3.6.2 bzw. den Kommentar nach Theorem 3.22.
- Hieraus ergibt sich (vgl. auch Beispiel 2 in
Abschnitt 4.3.1), daß für
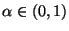
- Unter Berücksichtigung von (43) ergibt sich somit, daß
bzw.
- Also ist mit
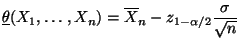 bzw. bzw.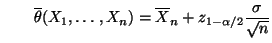 |
(44) |
ein Konfidenzintervall
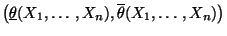 für
für 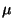 zum Niveau
zum Niveau
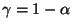 gegeben.
gegeben.
- Für die Länge
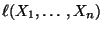 dieses Konfidenzintervalls
gilt
dieses Konfidenzintervalls
gilt
- Hieraus ergibt sich insbesondere, daß
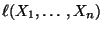 nicht
vom Zufall abhängt.
nicht
vom Zufall abhängt.
- Außerdem erkennen wir, daß die Länge
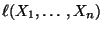 des in
(44) gegebenen Konfidenzintervalls klein ist, falls
das Niveau
des in
(44) gegebenen Konfidenzintervalls klein ist, falls
das Niveau
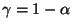 klein, die Varianz
klein, die Varianz 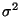 klein
bzw. der Stichprobenumfang
klein
bzw. der Stichprobenumfang  groß ist.
groß ist.
- Man kann sich leicht überlegen, daß
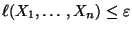 gilt, falls
gilt, falls
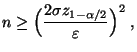 |
(45) |
wobei
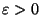 ein vorgegebener Schwellenwert ist.
ein vorgegebener Schwellenwert ist.
- Beachte
-




Next: Statistische Prüfverteilungen
Up: Konfidenzintervalle
Previous: Modellbeschreibung
Contents
Roland Maier
2001-08-20
![]() normalverteilt sind, d.h., es gelte
normalverteilt sind, d.h., es gelte