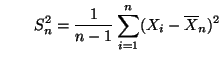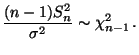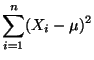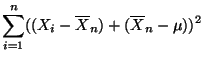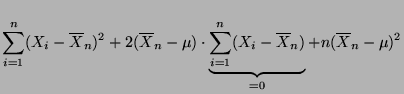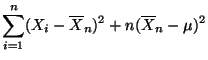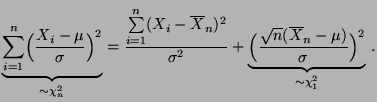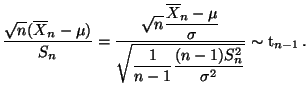Next: Weitere Konfidenzintervalle bei Normalverteilung
Up: Konfidenzintervalle
Previous: Konfidenzintervalle bei Normalverteilung; Quantilfunktion
Contents
Statistische Prüfverteilungen
Außer der Quantilfunktion der Standardnormalverteilung werden bei
der Bestimmung von Konfidenzintervallen bei normalverteilten
Stichprobenvariablen die Quantilfunktionen weiterer Verteilungen
benötigt.
Dabei werden insbesondere sogenannte Prüfverteilungen
betrachtet, die wie folgt definiert sind.
- Definition 5.22
 Seien
Seien
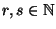 beliebige Zahlen und seien
beliebige Zahlen und seien
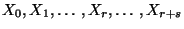 unabhängige und
N
unabhängige und
N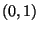 -verteilte Zufallsvariable. Dann heißt die Verteilung von
-verteilte Zufallsvariable. Dann heißt die Verteilung von
Die Theoreme 3.22 bzw. 3.23 weisen einen Weg, wie man ausgehend
von der in (3.6) eingeführten Dichte der
Standardnormalverteilung zu Formeln für die Dichten der
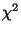 -Verteilung, t-Verteilung bzw. F-Verteilung gelangen kann.
Dabei ergibt sich insbesondere
-Verteilung, t-Verteilung bzw. F-Verteilung gelangen kann.
Dabei ergibt sich insbesondere
- Theorem 5.23
 Sei
Sei
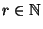 eine beliebige Zahl. Dann sind die Dichten der
Zufallsvariablen
eine beliebige Zahl. Dann sind die Dichten der
Zufallsvariablen
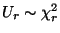 und
und 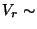 t
t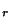 gegeben
durch
gegeben
durch
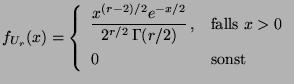 |
(46) |
bzw.
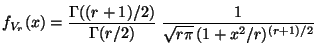 |
(47) |
für jedes
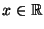 , wobei
, wobei
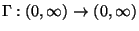 die
Gammafunktion mit
die
Gammafunktion mit
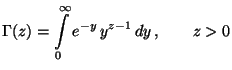 |
(48) |
bezeichnet;
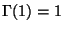 ,
,
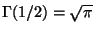 ,
,
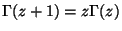 .
.
Wir bestimmen nun die (gemeinsame) Verteilung des
Stichprobenmittels
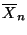 und der Stichprobenvarianz
und der Stichprobenvarianz
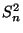 bei normalverteilten Stichprobenvariablen
bei normalverteilten Stichprobenvariablen
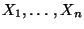 .
.
- Theorem 5.24
 Sei
Sei
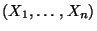 eine
normalverteilte Zufallsstichprobe mit
eine
normalverteilte Zufallsstichprobe mit 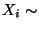 N
N
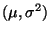 .
Dann sind
.
Dann sind
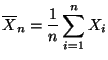
und
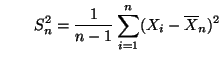
unabhängige Zufallsvariable, und es gilt
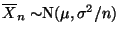 bzw. bzw.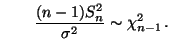 |
(49) |
- Beweis
-
- Der Nachweis der Unabhängigkeit von
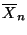 und
und 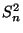 erfordert Hilfsmittel, die über den Rahmen dieser einführenden
Vorlesung hinausgehen.
erfordert Hilfsmittel, die über den Rahmen dieser einführenden
Vorlesung hinausgehen.
- Andererseits kann man sich leicht überlegen, daß
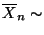 N
N
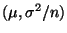 , vgl. das Beispiel in
Abschnitt 3.6.2 bzw. den Kommentar nach Theorem 3.22.
, vgl. das Beispiel in
Abschnitt 3.6.2 bzw. den Kommentar nach Theorem 3.22.
- Wir skizzieren hier lediglich eine Begründung für die Gültigkeit
von
- Offenbar gilt die Identität
- Hieraus ergibt sich, daß
- Weil die beiden Summanden auf der rechten Seite dieser Gleichung
unabhängig sind, ergibt sich nun aus der Definition der
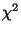 -Verteilung, daß der erste Summand auf der rechten Seite
-Verteilung, daß der erste Summand auf der rechten Seite
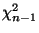 -verteilt ist.
-verteilt ist.
- Korollar 5.25
 Sei
Sei
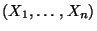 eine normalverteilte Zufallsstichprobe mit
eine normalverteilte Zufallsstichprobe mit
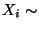 N
N
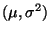 . Dann gilt
. Dann gilt
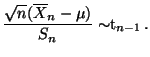 |
(50) |
- Beweis
 Weil die Zufallsvariablen
Weil die Zufallsvariablen
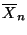 und
und 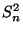 unabhängig
sind (vgl. Theorem 5.24), kann man sich leicht überlegen, daß auch
die Zufallsvariablen
unabhängig
sind (vgl. Theorem 5.24), kann man sich leicht überlegen, daß auch
die Zufallsvariablen
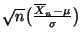 und
und
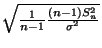 unabhängig sind.
Deshalb ergibt sich unmittelbar aus der Definition 5.22 der
t-Verteilung, daß
unabhängig sind.
Deshalb ergibt sich unmittelbar aus der Definition 5.22 der
t-Verteilung, daß
- Beachte
-




Next: Weitere Konfidenzintervalle bei Normalverteilung
Up: Konfidenzintervalle
Previous: Konfidenzintervalle bei Normalverteilung; Quantilfunktion
Contents
Roland Maier
2001-08-20


![]() -Verteilung, t-Verteilung bzw. F-Verteilung gelangen kann.
Dabei ergibt sich insbesondere
-Verteilung, t-Verteilung bzw. F-Verteilung gelangen kann.
Dabei ergibt sich insbesondere
![]() und der Stichprobenvarianz
und der Stichprobenvarianz
![]() bei normalverteilten Stichprobenvariablen
bei normalverteilten Stichprobenvariablen
![]() .
.
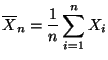 und
und