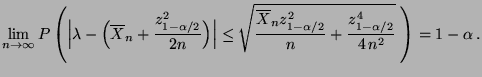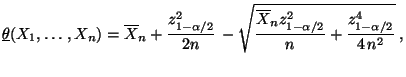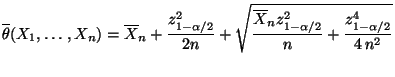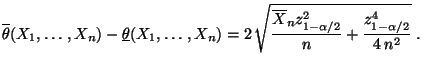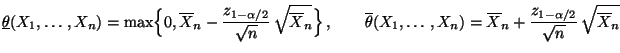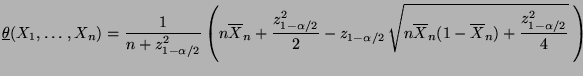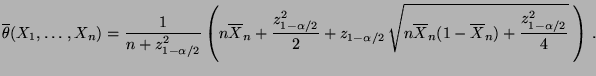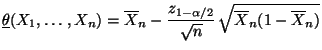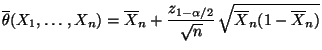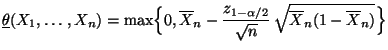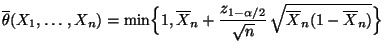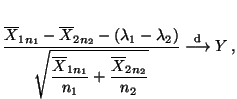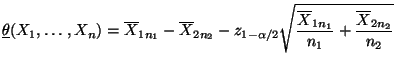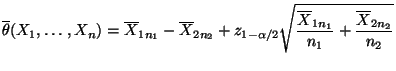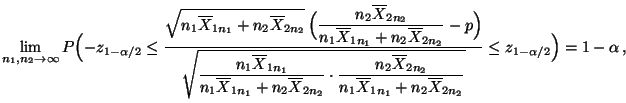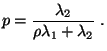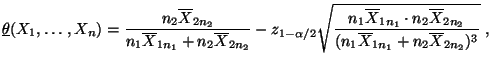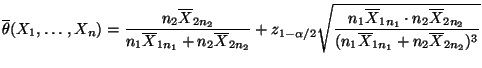Next: Tests statistischer Hypothesen
Up: Konfidenzintervalle
Previous: Zwei-Stichproben-Probleme
Contents
Asymptotische Konfidenzintervalle
Wir zeigen für zwei Beispiele von Familien parametrischer
Verteilungen, wie man mit Hilfe des zentralen Grenzwertsatzes
(vgl. Theorem 4.24) und des starken Gesetzes der großen Zahlen
(vgl. Theorem 4.22) asymptotische Konfidenzintervalle auf einfache
Weise herleiten kann.
Dabei kehren wir zunächst erneut zur Betrachtung von Ein-Stichproben-Problemen zurück. D.h., wir nehmen an, daß ein Datensatz
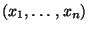 beobachtet wird, den wir als
Realisierung einer Zufallsstichprobe
beobachtet wird, den wir als
Realisierung einer Zufallsstichprobe
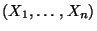 auffassen.
auffassen.
- Beispiel
 Konfidenzintervall für den Erwartungswert
Konfidenzintervall für den Erwartungswert 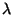 bei
Poisson-Verteilung
bei
Poisson-Verteilung
- Wir nehmen an, daß
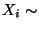 Poi
Poi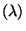 für ein (unbekanntes)
für ein (unbekanntes)
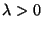 .
.
- Weil dann
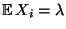 und
Var
und
Var 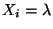 gilt, ergibt
sich aus Theorem 4.24, daß für jedes
gilt, ergibt
sich aus Theorem 4.24, daß für jedes
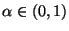
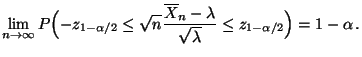 |
(64) |
- Durch Quadrierung der Ungleichungen in (64) und
anschließende Auflösung nach
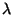 ergibt sich, daß
(64) äquivalent ist mit
ergibt sich, daß
(64) äquivalent ist mit
- Also ist mit
ein asymptotisches Konfidenzintervall
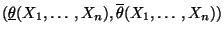 für
für 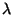 zum Niveau
zum Niveau
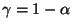 gegeben.
gegeben.
- Für die Länge dieses Konfidenzintervalls gilt
- Beachte
-
- Beispiel
 Konfidenzintervall für die ,,Erfolgswahrscheinlichkeit''
Konfidenzintervall für die ,,Erfolgswahrscheinlichkeit'' 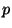 bei Bernoulli-Verteilung
bei Bernoulli-Verteilung
- Wir nehmen an, daß
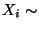 Bin
Bin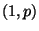 für ein (unbekanntes)
für ein (unbekanntes)
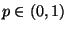 .
.
- Weil dann
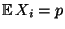 und
Var
und
Var 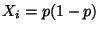 gilt, ergibt sich aus
Theorem 4.24, daß für jedes
gilt, ergibt sich aus
Theorem 4.24, daß für jedes
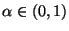
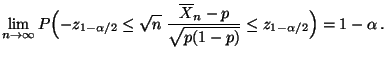 |
(67) |
- Durch Quadrierung der Ungleichungen in (67) und
anschließende Auflösung nach
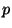 ergibt sich, daß
(67) äquivalent ist mit
wobei
bzw.
ergibt sich, daß
(67) äquivalent ist mit
wobei
bzw.
- Auf diese Weise ergibt sich ein asymptotisches Konfidenzintervall
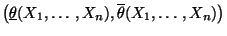 für
für 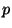 zum Niveau
zum Niveau
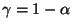 .
.
- Beachte
-
- Ähnlich wie in dem vorhergehenden Beispiel erhält man ein
einfacheres asymptotisches Konfidenzintervall für
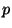 , wenn man
berücksichtigt, daß
wegen des starken Gesetzes der großen Zahlen (vgl. Theorem 4.22).
, wenn man
berücksichtigt, daß
wegen des starken Gesetzes der großen Zahlen (vgl. Theorem 4.22).
- Hieraus und aus (67) ergibt sich (wegen des Satzes
von Slutski), daß
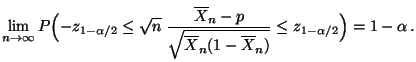 |
(68) |
- Also ist mit
bzw.
ein weiteres asymptotisches Konfidenzintervall
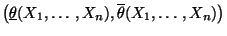 für
für 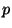 zum Niveau
zum Niveau
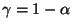 gegeben.
gegeben.
- Dieses Konfidenzinterval hat jedoch den Nachteil, daß die
Zufallsvariable
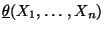 negative Werte
und
negative Werte
und
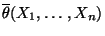 Werte größer als 1 annehmen
kann, obwohl bei der Bernoulli-Verteilung vorausgesetzt wird, daß
Werte größer als 1 annehmen
kann, obwohl bei der Bernoulli-Verteilung vorausgesetzt wird, daß
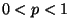 .
.
- Deshalb betrachtet man die modifizierten Schätzer
bzw.
als Endpunkte des Konfidenzintervalls
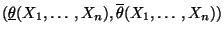 für
für 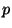 .
.
Wir betrachten nun noch zwei Beispiele für asymptotische
Konfidenzintervalle bei Zwei-Stichproben-Problemen.
- Seien
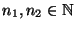 zwei beliebige, jedoch vorgegebene Zahlen.
zwei beliebige, jedoch vorgegebene Zahlen.
- So wie im ersten Teil des Abschnittes 5.3.5 fassen wir
die (konkreten) Stichproben
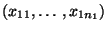 und
und
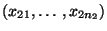 als Realisierungen von zwei
unabhängigen (d.h. nicht verbundenen) Zufallsstichproben
als Realisierungen von zwei
unabhängigen (d.h. nicht verbundenen) Zufallsstichproben
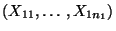 bzw.
bzw.
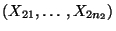 auf.
auf.
- Beispiel
 Konfidenzintervall für die Differenz zweier
Erwartungswerte (bei Poisson-Verteilung)
Konfidenzintervall für die Differenz zweier
Erwartungswerte (bei Poisson-Verteilung)
- Beispiel
 Konfidenzintervall für den Quotienten zweier
Erwartungswerte (bei Poisson-Verteilung)
Konfidenzintervall für den Quotienten zweier
Erwartungswerte (bei Poisson-Verteilung)
- So wie in dem vorhergehenden Beispiel nehmen wir an, daß
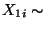 Poi
Poi
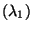 und
und
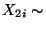 Poi
Poi
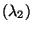 für (unbekannte)
für (unbekannte)
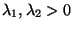 .
.
- Außerdem gelte für eine Zahl
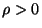
- Dann kann man zeigen, daß für jedes
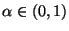 wobei
wobei
- Also ist mit
ein asymptotisches Konfidenzintervall
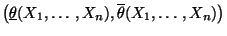 für
für 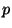 zum Niveau
zum Niveau
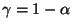 gegeben.
gegeben.




Next: Tests statistischer Hypothesen
Up: Konfidenzintervalle
Previous: Zwei-Stichproben-Probleme
Contents
Roland Maier
2001-08-20
![]() beobachtet wird, den wir als
Realisierung einer Zufallsstichprobe
beobachtet wird, den wir als
Realisierung einer Zufallsstichprobe
![]() auffassen.
auffassen.