



Next: Asymptotische Konfidenzintervalle
Up: Konfidenzintervalle
Previous: Weitere Konfidenzintervalle bei Normalverteilung
Contents
Zwei-Stichproben-Probleme
In Verallgemeinerung der Situation, die bisher in
Abschnitt 5 betrachtetet wurde, sollen nun gleichzeitig
zwei Datensätze
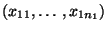 und
und
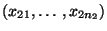 stochastisch modelliert werden.
stochastisch modelliert werden.
- Dabei können die Stichprobenumfänge
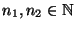 beliebige
Zahlen sein, die nicht notwendig gleich sein müssen.
beliebige
Zahlen sein, die nicht notwendig gleich sein müssen.
- Die (konkreten) Stichproben
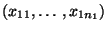 und
und
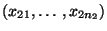 fassen wir als Realisierungen von zwei
Zufallsstichproben
fassen wir als Realisierungen von zwei
Zufallsstichproben
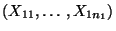 bzw.
bzw.
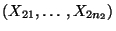 auf.
auf.
Wir betrachten nun zwei (unendliche) Folgen
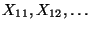 und
und
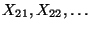 von Zufallsvariablen und nehmen an, daß
von Zufallsvariablen und nehmen an, daß
- die (zweidimensionalen) Zufallsvektoren
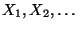 mit
mit
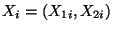 unabhängig und
identisch verteilt sind,
unabhängig und
identisch verteilt sind,
- die (gemeinsame) Verteilungsfunktion
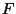 von
von  zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
zu
einer vorgegebenen parametrischen Familie von
Verteilungsfunktionen
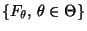 gehört,
gehört,
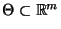 ,
,
- der Wahrscheinlichkeitsraum
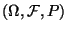 , über dem die
Zufallsvektoren
, über dem die
Zufallsvektoren
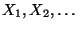 definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvektoren
ist.
definiert sind, der
kanonische Wahrscheinlichkeitsraum dieser Zufallsvektoren
ist.
- Beachte
 Die Komponenten
Die Komponenten 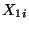 und
und 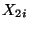 von
von  müssen jedoch
im allgemeinen weder unabhängig noch identisch verteilt sind.
müssen jedoch
im allgemeinen weder unabhängig noch identisch verteilt sind.
Im Rahmen dieser einführenden Vorlesung betrachten wir lediglich
den Fall, daß
- ein (nichtvektorieller) Funktionswert
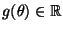 des Parametervektors
des Parametervektors
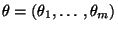 aus den beobachteten Daten
aus den beobachteten Daten
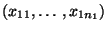 bzw.
bzw.
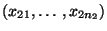 geschätzt werden soll, wobei
geschätzt werden soll, wobei
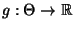 eine
vorgegebene Borel-meßbare Funktion sei.
eine
vorgegebene Borel-meßbare Funktion sei.
- Dabei diskutieren wir insbesondere die Frage, wie das
in Abschnitt 5.3.1
eingeführte Modell des Konfidenzintervalls verallgemeinert werden
kann, um zu Konfidenzintervallen ausgehend von (vektoriellen)
Stichprobenvariablen
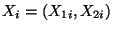 zu gelangen.
zu gelangen.
Zur Vereinfachung der Schreibweise setzen wir
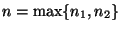 und
betrachten
und
betrachten
- Definition 5.26
 Sei
Sei
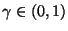 eine beliebige,
jedoch fest vorgegebene Zahl. Dann heißt das zufällige Intervall
eine beliebige,
jedoch fest vorgegebene Zahl. Dann heißt das zufällige Intervall
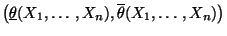 Konfidenzintervall für
Konfidenzintervall für 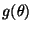 zum Niveau
zum Niveau
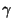 , falls
, falls
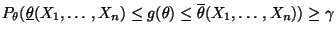 |
(61) |
für jedes
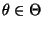 .
.
- Beachte
-
- Bisher hatten wir in Abschnit 5.3 stets den Fall
betrachtet, daß
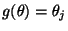 für ein
für ein
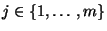 .
.
- In den folgenden Beispielen hat
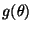 die Form
die Form
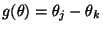 bzw.
bzw.
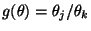 für ein vorgegebenes Paar
für ein vorgegebenes Paar
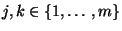 von Indizes.
von Indizes.
Die Stichprobenvariablen
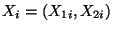 seien nun
normalverteilte Zufallsvektoren, wobei wir in den folgenden zwei
Beispielen außerdem voraussetzen, daß die Komponenten
seien nun
normalverteilte Zufallsvektoren, wobei wir in den folgenden zwei
Beispielen außerdem voraussetzen, daß die Komponenten 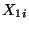 und
und
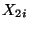 von
von  unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
- Beispiel
 Konfidenzintervall für die Differenz zweier
Erwartungswerte (bei bekannten Varianzen)
Konfidenzintervall für die Differenz zweier
Erwartungswerte (bei bekannten Varianzen)
- Beispiel
 Konfidenzintervall für den Quotienten zweier
Varianzen (bei unbekannten Erwartungswerten)
Konfidenzintervall für den Quotienten zweier
Varianzen (bei unbekannten Erwartungswerten)
- Beachte
-
- Beispiel
 Konfidenzintervall für die Differenz der Erwartungswerte von
verbundenen Stichproben
Konfidenzintervall für die Differenz der Erwartungswerte von
verbundenen Stichproben
- Beachte
-




Next: Asymptotische Konfidenzintervalle
Up: Konfidenzintervalle
Previous: Weitere Konfidenzintervalle bei Normalverteilung
Contents
Roland Maier
2001-08-20
![]() und
und
![]() stochastisch modelliert werden.
stochastisch modelliert werden.
![]() und
und
![]() von Zufallsvariablen und nehmen an, daß
von Zufallsvariablen und nehmen an, daß
![]() und
betrachten
und
betrachten
![]() seien nun
normalverteilte Zufallsvektoren, wobei wir in den folgenden zwei
Beispielen außerdem voraussetzen, daß die Komponenten
seien nun
normalverteilte Zufallsvektoren, wobei wir in den folgenden zwei
Beispielen außerdem voraussetzen, daß die Komponenten ![]() und
und
![]() von
von ![]() unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
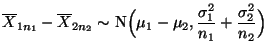
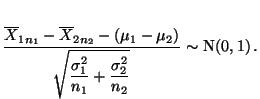
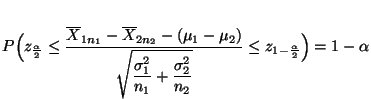
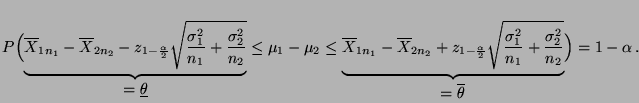
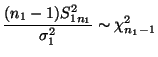 bzw.
bzw.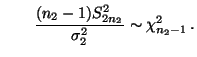
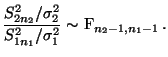
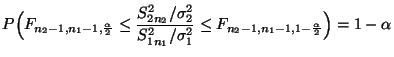
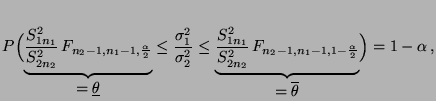
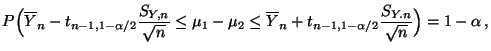
 und
und
 .
.