Next: Tabellen für Verteilungsfunktionen und
Up: Tests statistischer Hypothesen
Previous: Asymptotische Parametertests
Contents
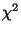 -Anpassungstest; Monte-Carlo-Simulation
-Anpassungstest; Monte-Carlo-Simulation
In diesem Abschnitt setzen wir nicht voraus, daß die Familie
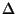 der insgesamt in Betracht gezogenen Verteilungsfunktionen
der insgesamt in Betracht gezogenen Verteilungsfunktionen
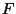 der Stichprobenvariablen
der Stichprobenvariablen  eine parametrische Familie von
Verteilungsfunktionen ist.
eine parametrische Familie von
Verteilungsfunktionen ist.
Wir vereinfachen deshalb die ursprüngliche Fragestellung
(90) auf die folgende Weise.
- Lemma 5.30
 Der in (91) definierte
Zufallsvektor
Der in (91) definierte
Zufallsvektor
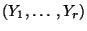 ist multinomialverteilt mit
den Parametern
ist multinomialverteilt mit
den Parametern
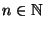 und
und
![$ p=(p_1,\ldots,p_{r-1})\in[0,1]^{r-1}$](img1904.png) , d.h., für beliebige
Zahlen
, d.h., für beliebige
Zahlen
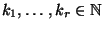 mit
mit
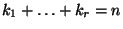 gilt
gilt
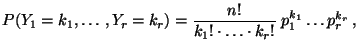 |
(92) |
wobei
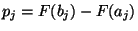 für jedes
für jedes
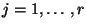 .
.
- Beweis
 Weil die Stichprobenvariablen
Weil die Stichprobenvariablen
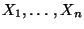 unabhängig und identisch verteilt sind (mit der
Verteilungsfunktion
unabhängig und identisch verteilt sind (mit der
Verteilungsfunktion 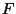 ), gilt
für jede Folge von Intervallen
), gilt
für jede Folge von Intervallen
![$ (a_{i_1},b_{i_1}],\ldots,(a_{i_n},b_{i_n}]$](img1911.png) . Hieraus ergibt sich
(92) durch Permutation der Stichprobenvariablen.
. Hieraus ergibt sich
(92) durch Permutation der Stichprobenvariablen.
- Beachte
-
Anstelle die ursprüngliche Fragestellung (90) zu
untersuchen, testen wir nun
- Beachte
-
- Als der ,,Entdecker'' des Grenzwertsatzes (94) gilt der
britische Statistiker Karl Pearson (1857-1936).
- Der asymptotische Test (95), der auf dem Grenzwertsatz
(94) beruht, heißt
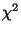 -Anpassungstest.
-Anpassungstest.
Wie das folgende Beispiel zeigt, kann der 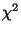 -Anpassungstest
zur Überprüfung der Güte von Zufallszahlengeneratoren bei der
Monte-Carlo-Simulation verwendet werden.
-Anpassungstest
zur Überprüfung der Güte von Zufallszahlengeneratoren bei der
Monte-Carlo-Simulation verwendet werden.
- Beispiel
 Test auf Gleichverteilung
Test auf Gleichverteilung
Für
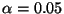 ,
,
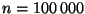 und
und 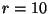 wollen wir nun prüfen,
ob
wollen wir nun prüfen,
ob
- die Hypothese der Gleichverteilung mit einer (konkreten)
Stichprobe
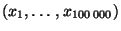 von Pseudozufallszahlen
vereinbar ist, für die sich der folgende Vektor der
Klassenhäufigkeiten
von Pseudozufallszahlen
vereinbar ist, für die sich der folgende Vektor der
Klassenhäufigkeiten
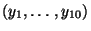 ergibt:
ergibt:
- In diesem Fall ist
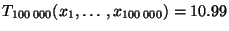 ,
und es gilt somit
wobei das Quantil
,
und es gilt somit
wobei das Quantil
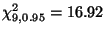 aus Tabelle 2
entnommen wurde.
aus Tabelle 2
entnommen wurde.
- Die Hypothese der Gleichverteilung wird also nicht verworfen.
Bei der Überprüfung der Güte von Zufallszahlengeneratoren sind
nicht nur Tests auf Gleichverteilung von Interesse. Ein weiteres
Gütekriterium besteht darin, ob die von einem
Zufallszahlengenerator erzeugten Pseudozufallszahlen
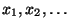 als Realisierungen unabhängiger
Zufallsvariablen
als Realisierungen unabhängiger
Zufallsvariablen
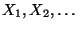 angesehen werden können.
angesehen werden können.
Der folgende Test auf Unabhängigkeit führt erneut zur Konstruktion
eines 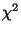 -Anpassungstests.
-Anpassungstests.
- Beispiel
 Test auf Unabhängigkeit (Run-Test)
Test auf Unabhängigkeit (Run-Test)
- Wir wollen nun prüfen, ob die Pseudozufallszahlen
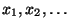 als Realisierungen von unabhängigen Zufallsvariablen
als Realisierungen von unabhängigen Zufallsvariablen
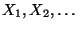 angesehen werden können, die gleichverteilt im
Intervall
angesehen werden können, die gleichverteilt im
Intervall ![$ (0,1]$](img1929.png) sind.
sind.
- Hierfür definieren wir die Zufallsvariablen
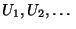 rekursiv durch
rekursiv durch
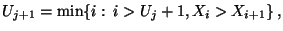 |
(96) |
wobei
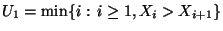 .
.
- Die Zufallsvariablen
 mit
mit
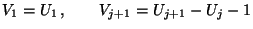 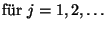 |
(97) |
werden dann die Runs der Folge
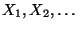 genannt.
genannt.
- Man kann zeigen, daß die in (97) eingeführten
Zufallsvariablen
 unabhängig und identisch
verteilt sind mit
unabhängig und identisch
verteilt sind mit
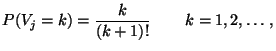 |
(98) |
falls die Zufallsvariablen
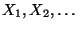 unabhängig und
(identisch) gleichverteilt im Intervall
unabhängig und
(identisch) gleichverteilt im Intervall ![$ (0,1]$](img1929.png) sind.
sind.
- Es mögen nun hinreichend viele Pseudozufallszahlen
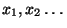 erzeugt werden, so daß sich aus ihnen gemäß (96) und
(97) die
erzeugt werden, so daß sich aus ihnen gemäß (96) und
(97) die  Runs
Runs
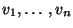 ergeben.
ergeben.
- Wir zerlegen die positive Halbachse in
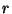 Intervalle
Intervalle
![$ (a_1,b_1],\ldots,(a_r,b_r]$](img1900.png) , so daß
, so daß
- die Wahrscheinlichkeiten
annähernd gleich sind, und
- für diese Wahrscheinlichkeiten betrachten wir den
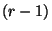 -dimensionalen (hypothetischen) Vektor
-dimensionalen (hypothetischen) Vektor
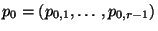 bzw.
bzw.
- die Testgröße
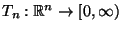 mit
wobei
mit
wobei
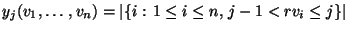 die Anzahl derjenigen Runlängen
die Anzahl derjenigen Runlängen
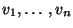 bezeichnet,
die in der
bezeichnet,
die in der 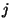 -ten Klasse liegen.
-ten Klasse liegen.
- Bei großem
 , was die Erzeugung entsprechend vieler
Pseudozufallszahlen
, was die Erzeugung entsprechend vieler
Pseudozufallszahlen
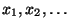 erfordert, wird die Hypothese
erfordert, wird die Hypothese
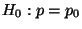 abgelehnt, falls
abgelehnt, falls
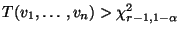 .
.




Next: Tabellen für Verteilungsfunktionen und
Up: Tests statistischer Hypothesen
Previous: Asymptotische Parametertests
Contents
Roland Maier
2001-08-20
![]() der insgesamt in Betracht gezogenen Verteilungsfunktionen
der insgesamt in Betracht gezogenen Verteilungsfunktionen
![]() der Stichprobenvariablen
der Stichprobenvariablen ![]() eine parametrische Familie von
Verteilungsfunktionen ist.
eine parametrische Familie von
Verteilungsfunktionen ist.
![$\displaystyle P\bigl(X_1\in(a_{i_1},b_{i_1}],\ldots,X_n\in(a_{i_n},b_{i_n}]\bigr)
=\prod\limits _{j=1}^n F(b_{i_j})-F(a_{i_j})
$](img1910.png)
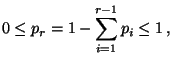
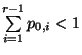 .
.
![]() -Anpassungstest
zur Überprüfung der Güte von Zufallszahlengeneratoren bei der
Monte-Carlo-Simulation verwendet werden.
-Anpassungstest
zur Überprüfung der Güte von Zufallszahlengeneratoren bei der
Monte-Carlo-Simulation verwendet werden.
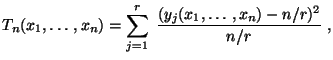
![]() ,
,
![]() und
und ![]() wollen wir nun prüfen,
ob
wollen wir nun prüfen,
ob
![]() als Realisierungen unabhängiger
Zufallsvariablen
als Realisierungen unabhängiger
Zufallsvariablen
![]() angesehen werden können.
angesehen werden können.
![]() -Anpassungstests.
-Anpassungstests.
![$\displaystyle p_{0,j}=\sum\limits
_{k\in\mathbb{N}\cap(a_j,b_j]}\frac{k}{(k+1)!}\,,\qquad j=1,\ldots,r
$](img1974.png)