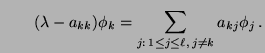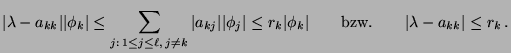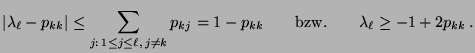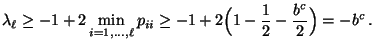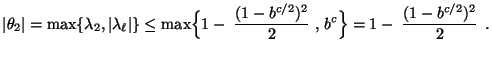- um obere Schranken für die Größe von
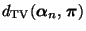 zu bestimmen, die sich im
zu bestimmen, die sich im 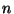 -ten
Iterationsschritt bei der MCMC-Simulation mit dem
Metropolis-Algorithmus ergibt,
-ten
Iterationsschritt bei der MCMC-Simulation mit dem
Metropolis-Algorithmus ergibt,
- wenn die zu simulierende Verteilung
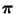 den folgenden
Bedingungen genügt.
den folgenden
Bedingungen genügt.
- dass
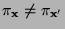 für beliebige
für beliebige
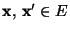 mit
mit
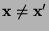 ,
,
- und dass die Zustände
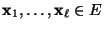 so
numeriert sind, dass
so
numeriert sind, dass
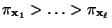 .
.
- wobei
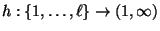 eine monoton wachsende
Funktion ist,
eine monoton wachsende
Funktion ist,
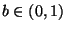 so gewählt wird, dass für eine gewisse Konstante
so gewählt wird, dass für eine gewisse Konstante 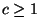
- und
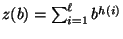 ein (im allgemeinen
unbekannter) Normierungsfaktor ist.
ein (im allgemeinen
unbekannter) Normierungsfaktor ist.
- dass die Basis
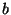 und die Differenzen
und die Differenzen
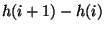 für jedes
für jedes
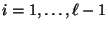 bekannt sind,
bekannt sind,
- d.h. insbesondere, dass die Quotienten
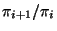 für jedes
für jedes
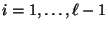 bekannt sind.
bekannt sind.
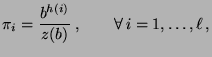
![$\displaystyle q_{ij}=\left\{\begin{array}{ll} \displaystyle\frac{1}{2}\;, &\mbo...
...\ell-1$\ und $j=i-1,\,i+1$,}\\ [3\jot] 0\,, & \mbox{sonst.} \end{array}\right.$](img1702.png)
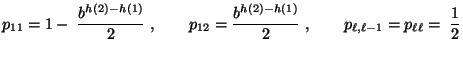
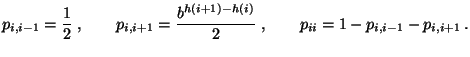
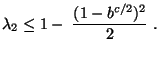
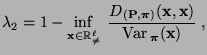
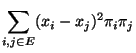
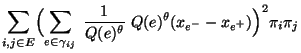
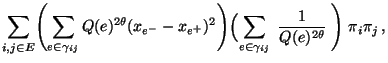
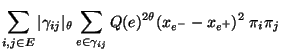
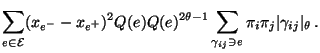
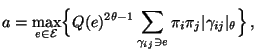
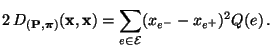
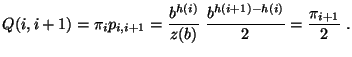
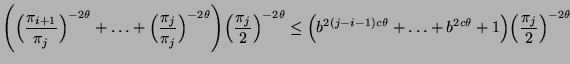
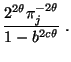
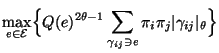
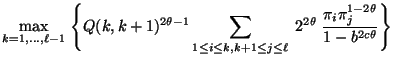
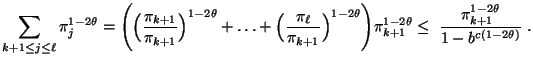
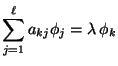 bzw.
bzw.