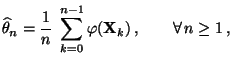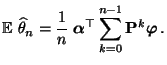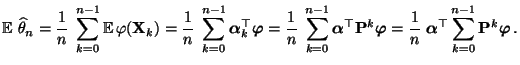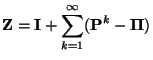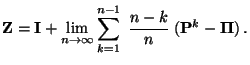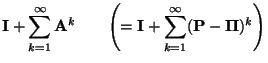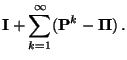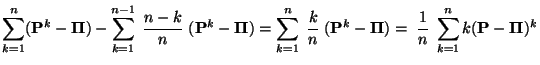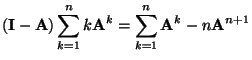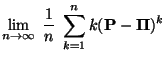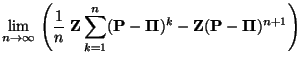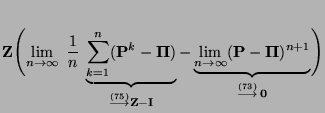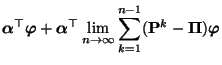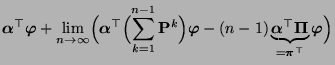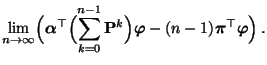Nächste Seite: Asymptotische Schätzvarianz; mittlerer quadratischer
Aufwärts: Fehleranalyse bei MCMC-Simulation
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit
Inhalt
MCMC-Schätzer; Bias und Fundamentalmatrix
In diesem Abschnitt betrachten wir Güteeigenschaften von
Monte-Carlo-Schätzern für Erwartungswerte.
- Beispiele für ähnliche Fragestellungen wurden bereits in
Abschnitt 3.1.1 diskutiert,
- und zwar im Zusammenhang mit der statistischen Schätzung der Zahl
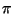
- bzw. des Wertes von Integralen mittels Monte-Carlo-Simulation.
- Dabei hatten wir in Abschnitt 3.1.1 jedoch
vorausgesetzt,
- dass die verwendeten Pseudozufallszahlen als Realisierungen von
unabhängigen und identisch verteilten Stichprobenvariablen
aufgefasst werden können,
- wogegen wir jetzt annehmen, dass die Stichprobenvariablen eine
(geeignet gewählte) Markov-Kette bilden.
- Deshalb sprechen wir nun auch von Markov-Chain-Monte-Carlo-Schätzern bzw. kurz von MCMC-Schätzern.
- Statistisches Modell
-
- Beachte
-
- Weil die Anfangsverteilung
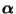 typischerweise nicht
mit der zu simulierenden Verteilung
typischerweise nicht
mit der zu simulierenden Verteilung
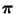 übereinstimmt,
übereinstimmt,
- ist der in (70) definierte MCMC-Schätzer
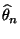 bei fest vorgegebenem (endlichen)
Stichprobenumfang
bei fest vorgegebenem (endlichen)
Stichprobenumfang 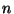 nicht erwartungstreu,
nicht erwartungstreu,
- d.h., im allgemeinen gilt
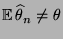 für
jedes
für
jedes 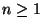 .
.
- Bei der Bestimmung des Bias
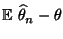 ist die folgende Darstellungsformel nützlich.
ist die folgende Darstellungsformel nützlich.
- Beweis
-
- Beachte
-
- Aus Theorem 3.17 und aus der Ergodizität der
Übergangsmatrix
 ergibt sich unter Berücksichtigung von
(69) sofort, dass
ergibt sich unter Berücksichtigung von
(69) sofort, dass
- d.h., der in (70) definierte MCMC-Schätzer
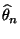 für
für 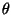 ist asymptotisch erwartungstreu.
ist asymptotisch erwartungstreu.
Außerdem kann die Asymptotik des Ausdruckes
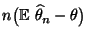 für
für
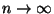 bestimmt werden. Hierfür leiten wir zunächst zwei elementare
Hilfssätze her.
bestimmt werden. Hierfür leiten wir zunächst zwei elementare
Hilfssätze her.
Lemma 3.2

Sei
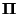
die
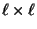
Matrix, die aus den
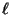
identischen (Zeilen-) Vektoren
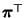
besteht. Dann gilt
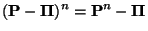 |
(72) |
für jedes
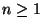
und insbesondere
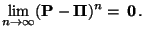 |
(73) |
- Beweis
-
- Beachte
-
Lemma 3.3

Für die Fundamentalmatrix
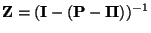
der
irreduziblen und aperiodischen Übergangsmatrix

gelten die
Darstellungsformeln
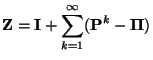 |
(75) |
und
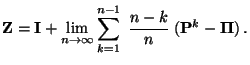 |
(76) |
- Beweis
-
- Die Gültigkeit von (75) ergibt sich aus den
Lemma 2.4 und Lemma 3.2, denn für
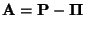 gilt, dass
gilt, dass
- Um die Gültigkeit von (76) zu zeigen, genügt es zu
beachten, dass
und dass der letzte Ausdruck gegen
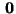 strebt, wenn
strebt, wenn
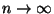 .
.
- Dabei ergibt sich diese Null-Konvergenz aus der Tatsache, dass
jede
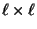 Matrix
Matrix
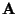 der Identität
genügt und dass somit für
der Identität
genügt und dass somit für
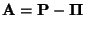

Mit Hilfe von Theorem 3.17 und Lemma 3.3
können wir nun das asymptotische Verhalten des Bias
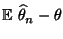 genauer bestimmen.
genauer bestimmen.
- Beweis
-
- Aus der Darstellungsformel (75) in
Lemma 3.3 ergibt sich, dass
- Hieraus und aus Theorem 3.17 ergibt sich für eine
gewisse Folge
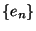 mit
mit 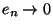 , dass
, dass





Nächste Seite: Asymptotische Schätzvarianz; mittlerer quadratischer
Aufwärts: Fehleranalyse bei MCMC-Simulation
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit
Inhalt
Ursa Pantle
2003-09-29