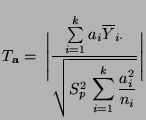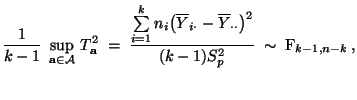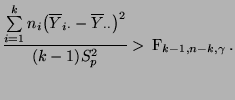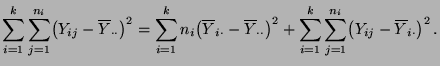- Die ANOVA-Nullhypothese
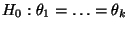 ist
äquivalent mit der Hypothese
ist
äquivalent mit der Hypothese
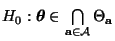 , wobei
, wobei
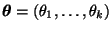 und
und
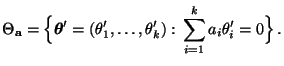
- Für jeden (einzelnen) Kontrast
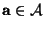 hatten wir in
Abschnitt 3.2.3 die Hypothese
hatten wir in
Abschnitt 3.2.3 die Hypothese
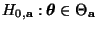 zum Niveau
zum Niveau
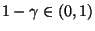 (gegen die
Alternative
(gegen die
Alternative
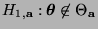 ) getestet.
) getestet.
- Dabei wurde die Nullhypothese
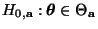 abgelehnt, falls die Testgröße
abgelehnt, falls die Testgröße
einen gewissen Schwellenwert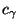 überschreitet, der nur von
überschreitet, der nur von
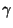 (jedoch nicht von
(jedoch nicht von
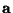 ) abhängt.
) abhängt.
- Weil
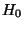 genau dann abgelehnt wird, wenn die Hypothese
genau dann abgelehnt wird, wenn die Hypothese
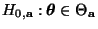 für ein
für ein
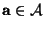 abgelehnt wird und
abgelehnt wird und
- weil somit der Ablehnungsbereich der ANOVA-Nullhypothese
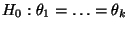 die Vereinigung der
Ablehnungsbereiche der Hypothesen
die Vereinigung der
Ablehnungsbereiche der Hypothesen
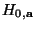 ist,
ist,
- ist es naheliegend, die Hypothese
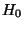 genau dann abzulehnen,
wenn
genau dann abzulehnen,
wenn
wobei der Schwellenwert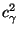 so gewählt wird, dass die
Wahrscheinlichkeit des in (47) betrachteten
Ereignisses unter
so gewählt wird, dass die
Wahrscheinlichkeit des in (47) betrachteten
Ereignisses unter 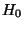 nicht größer als
nicht größer als 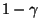 ist.
ist.
wobei
- Durch die folgende Quadratsummenzerlegung ergibt sich eine anschauliche Deutung von Zähler und Nenner der in (49) betrachteten Testgröße.
- Man kann nämlich zeigen, dass
- Die Doppelsumme auf der linken Seite von (50) kann
als eine Maßzahl für die (Gesamt-) Variabilität der
Stichprobenvariablen
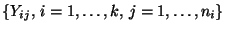 aufgefasst werden.
aufgefasst werden.
- Die erste Summe auf der rechten Seite von (50) ist eine Maßzahl für die Variabilität zwischen den Stufen des Einflussfaktors, während die Doppelsumme auf der rechten Seite von (50) eine Maßzahl für die Variabilität innerhalb der Stufen des Einflussfaktors ist.
- Wegen
ist die in (49) betrachtete Testgröße also proportional zu dem Quotienten, der aus der Variabilität zwischen den Stufen des Einflussfaktors und der Variabilität innerhalb der Stufen gebildet wird.
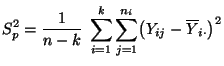
- Die durch (49) gegebene Entscheidungsregel bedeutet
somit, dass die ANOVA-Nullhypothese
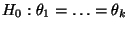 abgelehnt wird, falls die Variabilität zwischen den Stufen
signifikant größer als die Variabilität innerhalb der Stufen des
Einflussfaktors ist.
abgelehnt wird, falls die Variabilität zwischen den Stufen
signifikant größer als die Variabilität innerhalb der Stufen des
Einflussfaktors ist.
- Für das bereits in den Abschnitten 3.2.1 bzw.
3.2.3 betrachtete Beispiel der Eingabe von Wörtern
über drei verschiedene Tastaturen wollen wir nun prüfen, ob sich
die drei Tastaturen hinsichtlich der jeweils erwarteten Anzahlen
der eingegebenen Wörter je Minute signifikant voneinander
unterscheiden (
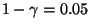 ).
).
- Mit anderen Worten: Wir testen die ANOVA Nullhypothese
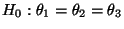 zum Niveau
zum Niveau
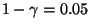 .
.
- Hierfür berechnen wir zunächst den beobachteten Wert der Testgröße
in (49), wobei sich für die Schätzer
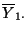 ,
,
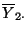 ,
,
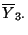 ,
,
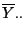 und
und 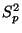 die folgenden Werte
ergeben:
und somit
die folgenden Werte
ergeben:
und somit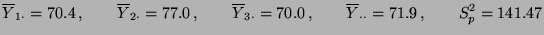
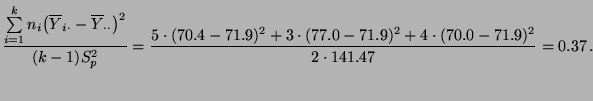
- Andererseits gilt
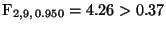 , weshalb
, weshalb
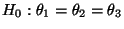 nicht abgelehnt wird.
nicht abgelehnt wird.