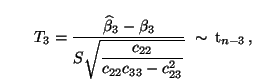Next: Güte der Modellanpassung; Overall-F-Test
Up: Multiple lineare Regression
Previous: Vektor- bzw. Matrixschreibweise
Contents
t-Tests und Konfidenzintervalle für
Regressionskonstante und Regressionskoeffizienten
- Zusätzlich zu den Modellannahmen, die bisher in
Abschnit 3.3 gemacht wurden, setzen wir nun voraus,
dass die zufälligen Störgrößen
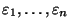 normalverteilt
sind. Wegen (53) gilt somit
normalverteilt
sind. Wegen (53) gilt somit
 |
(68) |
- Ähnlich wie bei den t-Tests, die in Abschnitt 3.1.3
für das einfache lineare Regressionsmodell betrachtet wurden,
können wir dann Hypothesen über einzelne Komponenten des
Parametervektors
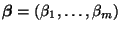 testen:
testen:
- Beachte
- Beispiel
- Für den bereits in Abschnitt 3.3.2 betrachteten
Spezialfall von zwei Einflussfaktoren, d.h.
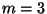 , lassen sich die
in (69) betrachteten Testgrößen
, lassen sich die
in (69) betrachteten Testgrößen 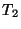 und
und 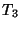 in
der folgenden Form schreiben:
in
der folgenden Form schreiben:
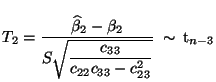 bzw. bzw.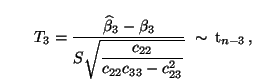 |
(73) |
wobei die Größen 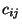 und
und 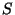
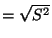 in
(58) bzw. (62) gegeben sind.
in
(58) bzw. (62) gegeben sind.
- Wir betrachten nun erneut den in Abschnitt 3.3.2
gegebenen Beispiel-Datensatz und prüfen, ob die Zielvariable
,,Stahlausbeute'' statistisch signifikant von den beiden
technologischen Einflussfaktoren ,,Anzahl der bisherigen
Abstiche'' und ,,Schefelgehalt'' des Produktionsprozesses abhängt.
- Mit anderen Worten: Wir verifizieren die Hypothesen
- In Abschnitt 3.3.2 hatten wir gezeigt, dass
- Durch Einsetzen in (73) ergeben sich nun unter
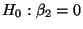 bzw.
bzw.
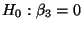 die folgenden ,,Testwerte''
zum Niveau
die folgenden ,,Testwerte''
zum Niveau
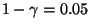 :
:
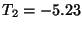
bzw.
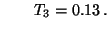
- Weil
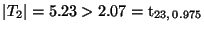 gilt, wird die
Null-Hypothese
gilt, wird die
Null-Hypothese
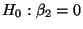 verworfen, d.h., die
Qualitätskennzahl ,,Stahlausbeute'' hängt statistisch
signifikant von dem ersten technlogischen Einflussfaktor ,,Anzahl
der bisherigen Abstiche'' ab.
verworfen, d.h., die
Qualitätskennzahl ,,Stahlausbeute'' hängt statistisch
signifikant von dem ersten technlogischen Einflussfaktor ,,Anzahl
der bisherigen Abstiche'' ab.
- Andererseits gilt
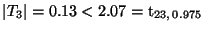 , d.h.,
die Abhängigkeit der Qualitätskennzahl ,,Stahlausbeute'' von dem
zweiten technlogischen Einflussfaktor ,,Schwefelgehalt'' ist
statistisch nicht gesichert.
, d.h.,
die Abhängigkeit der Qualitätskennzahl ,,Stahlausbeute'' von dem
zweiten technlogischen Einflussfaktor ,,Schwefelgehalt'' ist
statistisch nicht gesichert.
- Aus (73) ergeben sich darüber hinaus die
Konfidenzintervalle
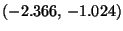 und
und
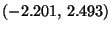 für
für
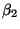 bzw.
bzw. 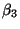 , wenn dabei das Konfidenzniveau
, wenn dabei das Konfidenzniveau
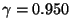 betrachtet wird.
betrachtet wird.




Next: Güte der Modellanpassung; Overall-F-Test
Up: Multiple lineare Regression
Previous: Vektor- bzw. Matrixschreibweise
Contents
Hendrik Schmidt
2003-07-21
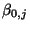 der
der 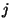 -ten Komponente
-ten Komponente
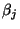 des Parametervektors
des Parametervektors
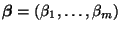 zu testen, betrachten wir dabei die Testgröße
zu testen, betrachten wir dabei die Testgröße
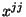 die
die 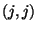 -te Eintragung der (inversen) Matrix
-te Eintragung der (inversen) Matrix
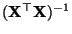 bezeichnet;
bezeichnet;
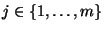 .
. 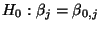 zum Niveau
zum Niveau
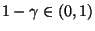 (gegen die Alternative
(gegen die Alternative
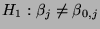 ) wird die Nullhypothese
) wird die Nullhypothese 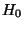 abgelehnt, falls
abgelehnt, falls
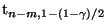 das
das
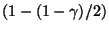 -Quantil der t-Verteilung mit
-Quantil der t-Verteilung mit 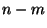 Freiheitsgraden bezeichnet.
Freiheitsgraden bezeichnet.
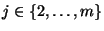 ist der Test der Hypothese
ist der Test der Hypothese
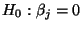 (gegen die Alternative
(gegen die Alternative
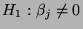 ) von
besonderem Interesse, weil damit verifiziert werden kann,
inwieweit die Zielvariablen
) von
besonderem Interesse, weil damit verifiziert werden kann,
inwieweit die Zielvariablen
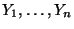 statistisch
signifikant von dem
statistisch
signifikant von dem 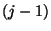 -ten Einflussfaktor abhängen.
-ten Einflussfaktor abhängen.
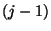 -ten Einflussfaktors
wird die Nullhypothese
-ten Einflussfaktors
wird die Nullhypothese 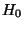 abgelehnt, falls
abgelehnt, falls
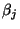 zum Niveau
zum Niveau
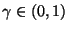 :
:
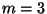 , lassen sich die
in (69) betrachteten Testgrößen
, lassen sich die
in (69) betrachteten Testgrößen 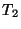 und
und 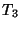 in
der folgenden Form schreiben:
in
der folgenden Form schreiben:
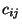 und
und 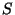
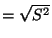 in
(58) bzw. (62) gegeben sind.
in
(58) bzw. (62) gegeben sind.
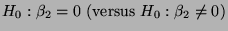 bzw.
bzw. 

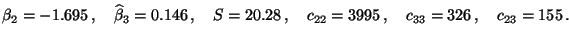
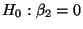 bzw.
bzw.
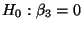 die folgenden ,,Testwerte''
zum Niveau
die folgenden ,,Testwerte''
zum Niveau
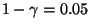 :
:
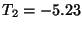 bzw.
bzw.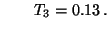
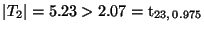 gilt, wird die
Null-Hypothese
gilt, wird die
Null-Hypothese
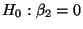 verworfen, d.h., die
Qualitätskennzahl ,,Stahlausbeute'' hängt statistisch
signifikant von dem ersten technlogischen Einflussfaktor ,,Anzahl
der bisherigen Abstiche'' ab.
verworfen, d.h., die
Qualitätskennzahl ,,Stahlausbeute'' hängt statistisch
signifikant von dem ersten technlogischen Einflussfaktor ,,Anzahl
der bisherigen Abstiche'' ab.
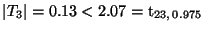 , d.h.,
die Abhängigkeit der Qualitätskennzahl ,,Stahlausbeute'' von dem
zweiten technlogischen Einflussfaktor ,,Schwefelgehalt'' ist
statistisch nicht gesichert.
, d.h.,
die Abhängigkeit der Qualitätskennzahl ,,Stahlausbeute'' von dem
zweiten technlogischen Einflussfaktor ,,Schwefelgehalt'' ist
statistisch nicht gesichert.
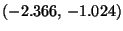 und
und
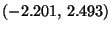 für
für
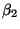 bzw.
bzw. 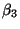 , wenn dabei das Konfidenzniveau
, wenn dabei das Konfidenzniveau
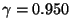 betrachtet wird.
betrachtet wird.
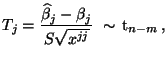
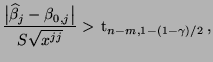
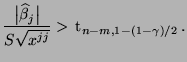
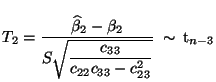 bzw.
bzw.