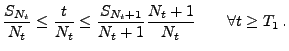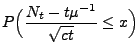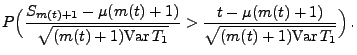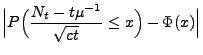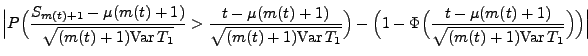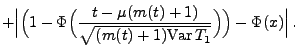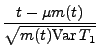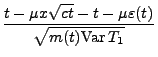Ergodensatz; Zentraler Grenzwertsatz

Aus dem starken Gesetz der großen Zahlen (vgl. Theorem WR-5.15) ergibt sich die folgende asymptotische Eigenschaft des Erneuerungsprozesses 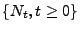$\{N_t,t\ge 0\}$; vgl. auch Beispiel 6 in Abschnitt WR-5.2.3. Aussagen dieses Typs werden in der Literatur individueller Ergodensatz genannt.

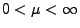
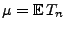
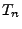
Theorem 2.1   Sei $0<\mu<\infty$, wobei $\mu={\mathbb{E}\,}T_n$ den Erwartungswert der Zwischenankunftszeiten $T_n$ bezeichnet. Dann gilt mit Wahrscheinlichkeit $1$, dass

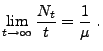$$\lim\limits_{t\to\infty}\frac{N_t}{t}=\frac{1}{\mu}\;.$$ (2)

Beweis

$\;$

• Für jedes 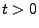$t>0$ gilt

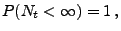  $$P(N_t<\infty)=1\,,$$ (3)

  
  
  denn aus Theorem WR-5.15 folgt, dass 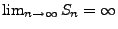$\lim_{n\to\infty} S_n=\infty$ mit Wahrscheinlichkeit 1.
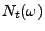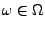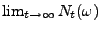• Außerdem ist $N_t(\omega)$ für jedes $\omega\in\Omega$ monoton nichtfallend in $t\ge 0$, d.h., der Grenzwert $\lim_{t\to\infty}N_t(\omega)$ existiert für jedes $\omega\in\Omega$.
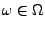• Darüber hinaus gilt mit Wahrscheinlichkeit 1

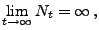  $$\lim_{t\to\infty}N_t=\infty\,,$$ (4)

  
  
  weil
  

  $$P\Bigl(\lim\limits_{t\to\infty}N_t<\infty\Bigr) = \lim\limits_{k\to\infty}P\Bigl(\lim\limits_{t\to\infty}N_t<k\Bigr)$$

  $$= \lim\limits_{k\to\infty}\lim\limits_{t\to\infty}P(N_t<k)$$

  $$= \lim\limits_{k\to\infty}\lim\limits_{t\to\infty}P(S_k>t)$$

  $$\le \lim\limits_{k\to\infty}\lim\limits_{t\to\infty} \Bigl(P(T_1>\frac{t}{k})+\ldots+P(T_k>\frac{t}{k})\Bigr)=0\,.$$

  
  

• Aus Theorem WR-5.15 folgt also, dass mit Wahrscheinlichkeit 1

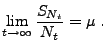  $$\lim\limits_{t\to\infty}\frac{S_{N_t}}{N_t}=\mu\;.$$ (5)

  
  

• Außerdem gilt für beliebige $t\ge 0$ und $n\in\mathbb{N}=\{1,2,\ldots\}$

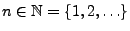
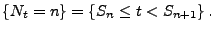  $$\{N_t=n\}=\{S_n\le t<S_{n+1}\}\,.$$ (6)

  
  

• Folglich gilt 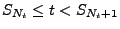$S_{N_t}\le t<S_{N_t+1}$ bzw.
  $$\frac{S_{N_t}}{N_t}\le\frac{t}{N_t}\le \frac{S_{N_t+1}}{N_t+1}\frac{N_t+1}{N_t}\qquad\forall t\ge T_1\,.$$

• Hieraus und aus (5) ergibt sich nun die Gültigkeit von (2).
  
  $\Box$

Außerdem gilt der folgende zentrale Grenzwertsatz; vgl. auch Beispiel 4 in Abschnitt WR-5.3.2.

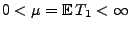
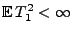
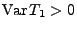
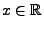
Theorem 2.2   Sei $0<\mu={\mathbb{E}\,}T_1<\infty$, ${\mathbb{E}\,}T_1^2<\infty$ und ${\rm Var\,}T_1>0$. Für jedes $x\in\mathbb{R}$ gilt dann

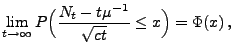$$\lim\limits_{t\to\infty}P\Bigl(\frac{N_t-t\mu^{-1}}{\sqrt{ct}}\le x\Bigr)=\Phi(x)\,,$$ (7)

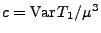
wobei $c={\rm Var\,}T_1/\mu^3$ und $\Phi:\mathbb{R}\to[0,1]$ die Verteilungsfunktion der Standardnormalverteilung ist.

Beweis

$\;$

• Aus dem Beweis des zentralen Grenzwertsatzes für Summen von unabhängigen und identisch verteilten Zufallsvariablen (vgl. den Beweis von Theorem WR-5.16) ergibt sich, dass die Konvergenz

  $$\lim\limits_{n\to\infty}P\Bigl(\frac{S_n-n\mu}{\sqrt{n{\rm Var\,} T_1}}\le x\Bigr)=\Phi(x)$$ (8)

  
  
  gleichmäßig in $x\in\mathbb{R}$ erfolgt.
• Sei $\lfloor a\rfloor$ der ganzzahlige Anteil von $a\ge 0$. Mit der Schreibweise $m(t)=\lfloor x\sqrt{ct}+t\mu^{-1}\rfloor$ gilt dann für jedes hinreichend große $t$
  

  $$P\Bigl(\frac{N_t-t\mu^{-1}}{\sqrt{ct}}\le x\Bigr) = P(N_t\le x\sqrt{ct}+t\mu^{-1})$$

  $$= P(S_{m(t)+1}> t)$$

  $$= P\Bigl(\frac{S_{m(t)+1}-\mu({m(t)+1})}{\sqrt{({m(t)+1}){\rm Var\,} T_1}}> \frac{t-\mu({m(t)+1})}{\sqrt{({m(t)+1}){\rm Var\,}T_1}}\Bigr)\,.$$

  
  

• Also gilt
  

  $${ \Bigl\vert P\Bigl(\frac{N_t-t\mu^{-1}}{\sqrt{ct}}\le x\Bigr)-\Phi(x)\Bigr\vert}$$

  $$\le \Bigl\vert P\Bigl(\frac{S_{m(t)+1}-\mu({m(t)+1})}{\sqrt{({m(t)+1}... ...( \frac{t-\mu({m(t)+1})}{\sqrt{({m(t)+1}){\rm Var\,}T_1}}\Bigr)\Bigr)\Bigr\vert$$

  $$+ \Bigl\vert\Bigl(1-\Phi\Bigl( \frac{t-\mu({m(t)+1})}{\sqrt{({m(t)+1}){\rm Var\,} T_1}}\Bigr)\Bigr)-\Phi(x)\Bigr\vert\,.$$

  
  

• Außerdem gilt für jedes $x\in\mathbb{R}$
  $$\lim\limits_{t\to\infty} m(t)=\lim\limits_{t\to\infty} \lfloor x\sqrt{ct}+t\mu^{-1}\rfloor=\infty\,.$$

• Wegen (8) und wegen der Symmetrieeigenschaft
  $$1-\Phi(-x)=\Phi(x)\qquad\forall x\in\mathbb{R}$$
  der Verteilungsfunktion $\Phi$ der N$(0,1)$-Verteilung genügt es somit noch zu zeigen, dass

  $$\lim\limits_{t\to\infty} \frac{t-\mu m(t)}{\sqrt{m(t){\rm Var\,} T_1}}=-x\,.$$ (9)

  
  

• Weil $m(t)=x\sqrt{ct}+t\mu^{-1}+\varepsilon(t)$ mit $0\le \vert\varepsilon(t)\vert< 1$ für jedes $t\ge 0$ gilt
  

  $$\frac{t-\mu m(t)}{\sqrt{m(t){\rm Var\,}T_1}} = \frac{t-\mu x\sqrt{ct}-t-\mu\varepsilon(t)}{\sqrt{m(t){\rm Var\,}T_1}}$$

  $$= -x\,\frac{\sqrt{\mu^{-1}{\rm Var\,}T_1 t}}{\sqrt{\mu^{-1}{\rm Var... ...\,} T_1\varepsilon(t)}}-\frac{\mu\varepsilon(t)}{\sqrt{m(t){\rm Var\,} T_1}}\;,$$

  
  
  wobei der erste Summand gegen $-x$ und der zweite Summand gegen 0 strebt für $t\to\infty$.
• Damit ist die Behauptung (7) bewiesen.
  
  $\Box$