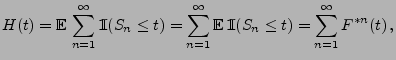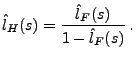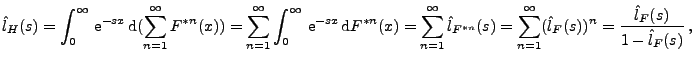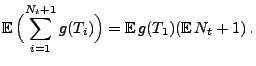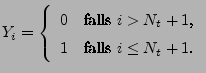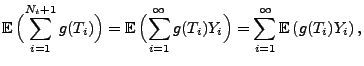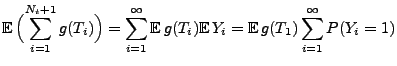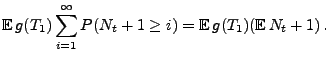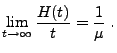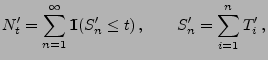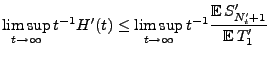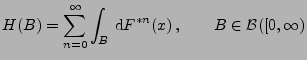Nächste Seite: Verzögerte Erneuerungprozesse; stationäre Zuwächse
Aufwärts: Zählprozesse; Erneuerungsprozesse
Vorherige Seite: Ergodensatz; Zentraler Grenzwertsatz
Inhalt
Erneuerungsfunktion
- Definition
 Die Funktion
Die Funktion
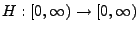 , wobei
, wobei
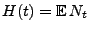 die erwartete Anzahl von Erneuerungszeitpunkten im Intervall
die erwartete Anzahl von Erneuerungszeitpunkten im Intervall
![$ [0,t]$](img222.png) bezeichnet, wird Erneuerungsfunktion von
bezeichnet, wird Erneuerungsfunktion von 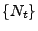 genannt. Aus (1) ergibt sich, dass
genannt. Aus (1) ergibt sich, dass
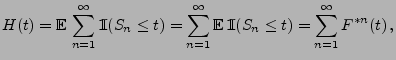 |
(10) |
wobei
![$ F:[0,\infty)\to[0,1]$](img225.png) die Verteilungsfunktion der
Zwischenankunftszeiten
die Verteilungsfunktion der
Zwischenankunftszeiten 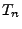 und
und 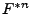 die
die 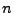 -te
Faltungspotenz von
-te
Faltungspotenz von 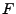 bezeichnet. Dabei gilt
bezeichnet. Dabei gilt
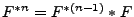 und
und
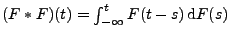 mit
mit
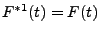 und
und
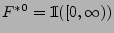 , d.h.,
, d.h.,
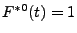 für
für  und
und
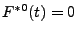 für
für 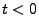 .
.
- Beachte

- Es ist klar, dass die Erneuerungsfunktion
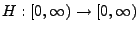 monoton wachsend ist. Außerdem ist es
nicht schwierig zu zeigen, dass
monoton wachsend ist. Außerdem ist es
nicht schwierig zu zeigen, dass
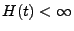 für jedes
für jedes  gilt.
gilt.
- Allerdings ist es nur in wenigen Spezialfällen möglich, einfache
geschlossene Formeln für die Erneuerungsfunktion
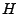 herzuleiten.
Die Laplace-Stieltjes-Transformierte
herzuleiten.
Die Laplace-Stieltjes-Transformierte
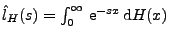 von
von 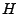 lässt sich jedoch immer
durch die Laplace-Stieltjes-Transformierte von
lässt sich jedoch immer
durch die Laplace-Stieltjes-Transformierte von 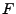 ausdrücken.
ausdrücken.
- Beweis
 Aus (10) ergibt sich, dass
wobei die geometrische Reihe
Aus (10) ergibt sich, dass
wobei die geometrische Reihe
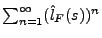 konvergiert, weil
konvergiert, weil
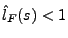 für jedes
für jedes 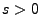 gilt.
gilt.

Aus Theorem 2.1 ergibt sich die Vermutung, dass die
Erneuerungsfunktion
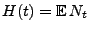 ein ähnliches asymptotisches
lineares Verhalten hat, wie es in (2) für den
Erneuerungsprozess
ein ähnliches asymptotisches
lineares Verhalten hat, wie es in (2) für den
Erneuerungsprozess 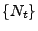 gezeigt wurde. Um dies zu zeigen,
benötigen wir den folgenden Hilfssatz, der in der Literatur die
Waldsche Identität für Erneuerungsprozesse genannt wird.
gezeigt wurde. Um dies zu zeigen,
benötigen wir den folgenden Hilfssatz, der in der Literatur die
Waldsche Identität für Erneuerungsprozesse genannt wird.
Lemma 2.1
Sei
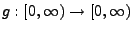
ein beliebige Borel-messbare
Funktion. Dann gilt für jedes
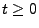
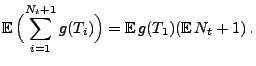 |
(12) |
- Beweis

Wir sind nun in der Lage, das folgende Theorem zu beweisen, das in
der Literatur der elementare Erneuerungssatz genannt wird.
- Beweis

Außer der in Theorem 2.4 hergeleiteten
asymptotischen Linearität lässt sich noch eine wesentliche
schärfere Aussage über das asymptotische Verhalten der
Erneuerungsfunktion 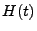 für
für
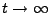 herleiten.
herleiten.
Der folgende Grenzwertsatz wird in der Literatur Erneuerungssatz von Blackwell bzw. Haupterneuerungssatz.
genannt. Er besagt, dass sich das Erneuerungsmaß
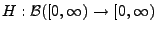 mit
mit
asymptotisch genauso wie das Lebesgue-Maß verhält.
Theorem 2.5
Sei
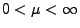
, und die Verteilungsfunktion
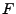
sei nicht
gitterförmig, d.h., die Wachstumspunkte von
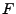
liegen nicht auf
einem regelmäßigen Gitter. Dann gilt
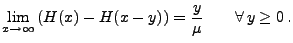 |
(16) |
Der Beweis von Theorem 2.5 geht über den
Rahmen dieser Vorlesung hinaus und wird deshalb weggelassen. Er
kann beispielsweise in Kallenberg (2001), S. 172-174 nachgelesen
werden .




Nächste Seite: Verzögerte Erneuerungprozesse; stationäre Zuwächse
Aufwärts: Zählprozesse; Erneuerungsprozesse
Vorherige Seite: Ergodensatz; Zentraler Grenzwertsatz
Inhalt
Ursa Pantle
2005-07-13
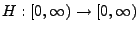 monoton wachsend ist. Außerdem ist es
nicht schwierig zu zeigen, dass
monoton wachsend ist. Außerdem ist es
nicht schwierig zu zeigen, dass
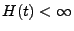 für jedes
für jedes  gilt.
gilt.
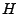 herzuleiten.
Die Laplace-Stieltjes-Transformierte
herzuleiten.
Die Laplace-Stieltjes-Transformierte
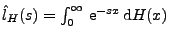 von
von 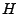 lässt sich jedoch immer
durch die Laplace-Stieltjes-Transformierte von
lässt sich jedoch immer
durch die Laplace-Stieltjes-Transformierte von 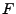 ausdrücken.
ausdrücken.