



Nächste Seite: Ergodensatz; Zentraler Grenzwertsatz
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Prozesse mit stückweise konstanten
Inhalt
Zählprozesse; Erneuerungsprozesse
Sei
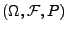 ein beliebiger Wahrscheinlichkeitsraum, und
sei
ein beliebiger Wahrscheinlichkeitsraum, und
sei
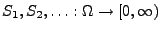 eine beliebige Folge von
nichtnegativen Zufallsvariablen mit
eine beliebige Folge von
nichtnegativen Zufallsvariablen mit
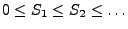 .
.
In der Versicherungsmathematik können die Zufallsvariablen 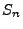 Zeitpunkte modellieren, zu denen Schäden eines bestimmten Typs
eintreten. Dies können beispielsweise Schäden sein, die durch
Naturkatastrophen wie Erdbeben oder schwere Stürme verursacht
werden.
Zeitpunkte modellieren, zu denen Schäden eines bestimmten Typs
eintreten. Dies können beispielsweise Schäden sein, die durch
Naturkatastrophen wie Erdbeben oder schwere Stürme verursacht
werden.
- Definition

- Der stochastische Prozess
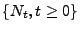 mit
mit
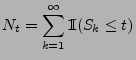 |
(1) |
wird Zählprozess genannt, wobei
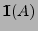 der Indikator des Ereignisses
der Indikator des Ereignisses
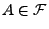 ist, d.h.
ist, d.h.
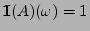 , falls
, falls
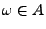 , und
, und
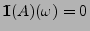 ,
falls
,
falls
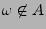 .
.
- Sei
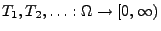 eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen, die nur
nichtnegative Werte annehmen.
eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen, die nur
nichtnegative Werte annehmen.
- Dann wird die Folge
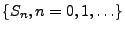 mit
mit 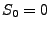 und
und
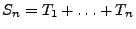 für
für 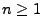 ein Erneuerungspunktprozess genannt, wobei
ein Erneuerungspunktprozess genannt, wobei 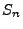 der
der 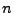 -te Erneuerungszeitpunkt heißt.
-te Erneuerungszeitpunkt heißt.
- Der in (1) gegebene stochastische Prozess
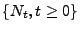 wird in diesem Fall Erneuerungszählprozess
bzw. kurz Erneuerungsprozess genannt.
wird in diesem Fall Erneuerungszählprozess
bzw. kurz Erneuerungsprozess genannt.
- Dabei wird stets vorausgesetzt, dass die
,,Zwischenankunftszeiten''
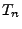 nicht mit Wahrscheinlichkeit 1
gleich Null sind, d.h., es gelte
nicht mit Wahrscheinlichkeit 1
gleich Null sind, d.h., es gelte
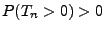 für jedes
für jedes 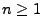 .
.
Unterabschnitte




Nächste Seite: Ergodensatz; Zentraler Grenzwertsatz
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Prozesse mit stückweise konstanten
Inhalt
Ursa Pantle
2005-07-13
![]() ein beliebiger Wahrscheinlichkeitsraum, und
sei
ein beliebiger Wahrscheinlichkeitsraum, und
sei
![]() eine beliebige Folge von
nichtnegativen Zufallsvariablen mit
eine beliebige Folge von
nichtnegativen Zufallsvariablen mit
![]() .
.
![]() Zeitpunkte modellieren, zu denen Schäden eines bestimmten Typs
eintreten. Dies können beispielsweise Schäden sein, die durch
Naturkatastrophen wie Erdbeben oder schwere Stürme verursacht
werden.
Zeitpunkte modellieren, zu denen Schäden eines bestimmten Typs
eintreten. Dies können beispielsweise Schäden sein, die durch
Naturkatastrophen wie Erdbeben oder schwere Stürme verursacht
werden.