



Nächste Seite: Poissonsche Zählmaße; Cox-Prozesse; Simluationsalgorithmus
Aufwärts: Zählprozesse vom Poisson-Typ
Vorherige Seite: Zusammengesetzte Poisson-Prozesse
Inhalt
Bedingte Erwartung und bedingte Wahrscheinlichkeit
Um den in Abschnitt 2.2.1 betrachteten Begriff des
(homogenen) Poissonschen Zählprozesses
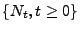 noch in
eine andere Richtung verallgemeinern zu können, benötigen wir als
Hilfsmittel die Begriffe der bedingten Erwartung bzw. der
bedingten Wahrscheinlichkeit bezüglich einer beliebigen
Teil-
noch in
eine andere Richtung verallgemeinern zu können, benötigen wir als
Hilfsmittel die Begriffe der bedingten Erwartung bzw. der
bedingten Wahrscheinlichkeit bezüglich einer beliebigen
Teil- -Algebra
-Algebra
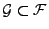 der
Ereignis-
der
Ereignis- -Algebra
-Algebra
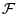 des zugrundeliegenden
Wahrscheinlichkeitsraumes
des zugrundeliegenden
Wahrscheinlichkeitsraumes
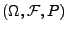 .
.
- Beachte

- Falls
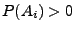 , dann ist die in (34) gegebene
Zahl
, dann ist die in (34) gegebene
Zahl
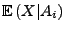 der bedingte Erwartungswert von
der bedingte Erwartungswert von 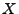 unter der
Bedingung
unter der
Bedingung 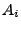 , d.h., der Erwartungswert bezüglich der bedingten Verteilung
, d.h., der Erwartungswert bezüglich der bedingten Verteilung
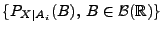 ,
wobei
,
wobei
- Von besonderer Wichtigkeit ist der Fall, dass die
 -Algebra
-Algebra
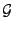 durch die Urbilder einer (diskreten)
Zufallsvariablen
durch die Urbilder einer (diskreten)
Zufallsvariablen  erzeugt wird, die nur endlich viele
verschiedene Werte mit positiver Wahrscheinlichkeit annimmt:
erzeugt wird, die nur endlich viele
verschiedene Werte mit positiver Wahrscheinlichkeit annimmt:
- Sei
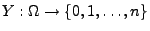 eine Zufallsvariable, die nur
die Werte
eine Zufallsvariable, die nur
die Werte
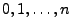 mit positiver Wahrscheinlichkeit annimmt,
beispielsweise eine binomialverteilte Zufallsvariable, und
mit positiver Wahrscheinlichkeit annimmt,
beispielsweise eine binomialverteilte Zufallsvariable, und
- sei
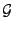 die
die  -Algebra
-Algebra
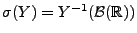 ,
d.h., die kleinste (endliche) Teil-
,
d.h., die kleinste (endliche) Teil- -Algebra von
-Algebra von
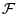 ,
die die Urbilder
,
die die Urbilder
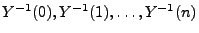 enthält,
enthält,
- dann wird die bedingte Erwartung
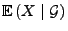 auch mit dem
Symbol
auch mit dem
Symbol
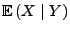 bezeichnet (und bedingte Erwartung von
bezeichnet (und bedingte Erwartung von 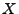 bezüglich
bezüglich  genannt).
genannt).
- Sei
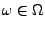 , so dass
, so dass
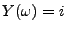 . Dann ist der
Funktionswert
. Dann ist der
Funktionswert
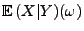 der Zufallsvariablen
der Zufallsvariablen
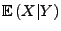 gegeben durch den bedingten Erwartungswert
wobei
gegeben durch den bedingten Erwartungswert
wobei
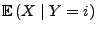 eine
Kurzschreibweise ist für
eine
Kurzschreibweise ist für
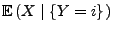 .
.
- Die bisher erläuterte Vorgehensweise bei der Definition der
bedingten Erwartung
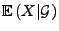 bezüglich einer (Teil-)
bezüglich einer (Teil-)
 -Algebra
-Algebra
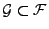 kann auch dann beibehalten
werden,
kann auch dann beibehalten
werden,
- wenn
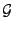 aus abzählbar unendlich vielen Teilmengen von
aus abzählbar unendlich vielen Teilmengen von
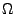 besteht,
besteht,
- d.h., wenn
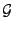 beispielsweise durch die Urbilder einer
Poisson-verteilten Zufallsvariablen erzeugt wird,
beispielsweise durch die Urbilder einer
Poisson-verteilten Zufallsvariablen erzeugt wird,
- wobei dann lediglich die endliche Summe in (33)
durch eine unendliche Summe ersetzt werden muss.
- Die folgenden Eigenschaften der bedingten Erwartung
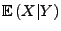 ergeben sich unmittelbar aus der Definitionsgleichungen
(33) und (34):
ergeben sich unmittelbar aus der Definitionsgleichungen
(33) und (34):
Die folgende (allgemeine) Definition der bedingten Erwartung
beruht auf dem Satz von Radon-Nikodym der Maß- und
Integrationstheorie. Sie enthält die oben betrachteten
Definitionsgleichungen (33) und (34)
als Spezialfall.
- Defintion
 Jede
Jede
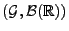 -messbare Abbildung
-messbare Abbildung
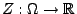 ,
für die (37) gilt, heißt eine Version der bedingten Erwartung von
,
für die (37) gilt, heißt eine Version der bedingten Erwartung von 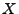 bezüglich
bezüglich
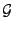 und wird mit
und wird mit
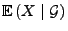 bezeichnet.
bezeichnet.
Aus der Definitionsgleichung (37) und aus den
allgemeinen Rechenregeln für das Lebesgue-Integral ergeben sich
die folgenden Eigenschaften der bedingten Erwartung, die wir hier
lediglich (ohne Beweis) erwähnen.
Theorem 2.11
Seien
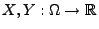
beliebige Zufallsvariablen über
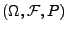
mit
und sei
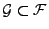
eine beliebige Teil-

-Algebra
von
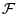
. Dann gilt
- 1.
-
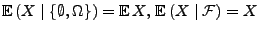 ,
,
- 2.
-
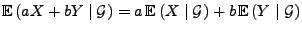 für
beliebige
für
beliebige
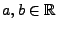 ,
,
- 3.
-
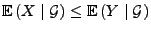 , falls
, falls 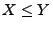 ,
,
- 4.
-
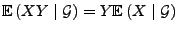 , falls
, falls  eine
eine
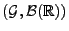 -messbare Zufallsvariable ist,
-messbare Zufallsvariable ist,
- 5.
-
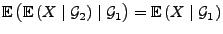 ,
falls
,
falls
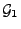 und
und
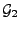 Teil-
Teil- -Algebren von
-Algebren von
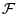 sind mit
sind mit
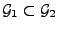 ,
,
- 6.
-
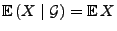 , falls die
, falls die  -Algebren
-Algebren
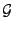 und
und
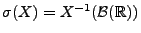 unabhängig sind, d.h., falls
unabhängig sind, d.h., falls
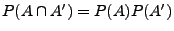 für beliebige
für beliebige
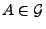 und
und
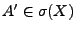 .
.
- 7.
-
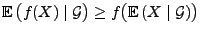 ,
falls
,
falls
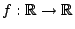 eine konvexe Funktion ist, so dass
eine konvexe Funktion ist, so dass
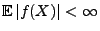 .
.
- Beachte
 Außerdem sind die folgenden Eigenschaften bzw. Schreib- und
Sprechweisen von Interesse.
Außerdem sind die folgenden Eigenschaften bzw. Schreib- und
Sprechweisen von Interesse.
- Unmittelbar aus der Definitionsgleichung (37)
ergibt sich, dass
-
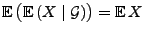 , wenn
, wenn 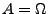 gesetzt
wird,
gesetzt
wird,
-
 für beliebige
für beliebige
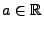 und
und
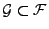 ,
,
-
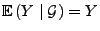 für jede
für jede
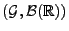 -messbare
Zufallsvariable
-messbare
Zufallsvariable  .
.
- Seien
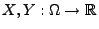 beliebige Zufallsvariablen über
beliebige Zufallsvariablen über
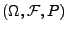 mit
mit
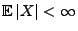 ,
,
- und sei
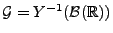 die Teil-
die Teil- -Algebra von
-Algebra von
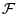 , die durch die Urbilder von
, die durch die Urbilder von  erzeugt wird.
erzeugt wird.
- Dann heißt
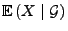 die bedingte Erwartung von
die bedingte Erwartung von 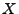 bezüglich
bezüglich  , wobei auch die Schreibweise
, wobei auch die Schreibweise
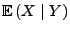 benutzt
wird.
benutzt
wird.
- Wenn es eine Borel-messbare Funktion
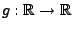 gibt, so dass
sich die bedingte Erwartung
gibt, so dass
sich die bedingte Erwartung
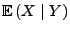 in der Form
in der Form
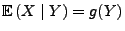 darstellen lässt, dann spricht man von regulärer
bedingter Erwartung.
darstellen lässt, dann spricht man von regulärer
bedingter Erwartung.
- Beispiele
-
- Absolutstetige Zufallsvektoren
- Funktionale unabhängiger Zufallsvariablen
- Funktionale unabhängiger stochastischer Prozesse
Schließlich erwähnen wir noch kurz den Begriff bedingter
Wahrscheinlichkeiten bezüglich  -Algebren.
-Algebren.
- Definition
-




Nächste Seite: Poissonsche Zählmaße; Cox-Prozesse; Simluationsalgorithmus
Aufwärts: Zählprozesse vom Poisson-Typ
Vorherige Seite: Zusammengesetzte Poisson-Prozesse
Inhalt
Ursa Pantle
2005-07-13
![]() noch in
eine andere Richtung verallgemeinern zu können, benötigen wir als
Hilfsmittel die Begriffe der bedingten Erwartung bzw. der
bedingten Wahrscheinlichkeit bezüglich einer beliebigen
Teil-
noch in
eine andere Richtung verallgemeinern zu können, benötigen wir als
Hilfsmittel die Begriffe der bedingten Erwartung bzw. der
bedingten Wahrscheinlichkeit bezüglich einer beliebigen
Teil-![]() -Algebra
-Algebra
![]() der
Ereignis-
der
Ereignis-![]() -Algebra
-Algebra
![]() des zugrundeliegenden
Wahrscheinlichkeitsraumes
des zugrundeliegenden
Wahrscheinlichkeitsraumes
![]() .
.
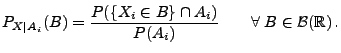
![]() -Algebren.
-Algebren.