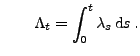Nächste Seite: Markow-Prozesse mit endlich vielen
Aufwärts: Zählprozesse vom Poisson-Typ
Vorherige Seite: Bedingte Erwartung und bedingte
Inhalt
Poissonsche Zählmaße; Cox-Prozesse; Simluationsalgorithmus
Der in Abschnitt 2.2.1 betrachtete Begriff des
Poissonschen Zählprozesses
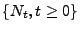 mit
mit
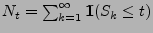 und
und
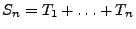 ,
wobei die Zufallsvariablen
,
wobei die Zufallsvariablen
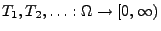 unabhängig und identisch Exp(
unabhängig und identisch Exp(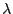 )-verteilt sind, lässt sich
wie folgt weiter verallgemeinern.
)-verteilt sind, lässt sich
wie folgt weiter verallgemeinern.
- Definition
 Das in (41) gegebene
zufällige Zählmaß
Das in (41) gegebene
zufällige Zählmaß
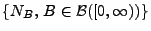 , wobei
, wobei
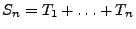 und die Zufallsvariablen
und die Zufallsvariablen
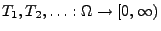 unabhängig und identisch
Exp(
unabhängig und identisch
Exp(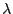 )-verteilt sind, wird homogenes Poissonsches
Zählmaß mit der Intensität
)-verteilt sind, wird homogenes Poissonsches
Zählmaß mit der Intensität 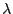 genannt.
genannt.
Unmittelbar aus Theorem 2.9 ergibt sich die
Gültigkeit der folgende beiden Aussagen.
- Beachte
 Mit Hilfe des Satzes über die monotone Konvergenz kann man leicht
zeigen, dass die Mengenfunktion
Mit Hilfe des Satzes über die monotone Konvergenz kann man leicht
zeigen, dass die Mengenfunktion
![$ \mu:\mathcal{B}([0,\infty))\to[0,\infty]$](img527.png) mit
mit
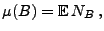 |
(43) |
die durch das zufällige Zählmaß
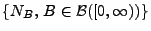 induziert wird,
induziert wird,
 -additiv ist, d.h.,
-additiv ist, d.h., 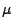 ist ein Maß.
ist ein Maß.
- Definition
 Das in (43) gegebene Maß
Das in (43) gegebene Maß 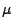 wird Intensitätsmaß des zufälligen Zählmaßes
wird Intensitätsmaß des zufälligen Zählmaßes 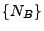 genannt.
genannt.
- Beachte

- Definition
 Sei
Sei
![$ \mu:\mathcal{B}([0,\infty))\to[0,\infty]$](img527.png) ein
beliebiges lokal-endliches Maß, d.h.,
ein
beliebiges lokal-endliches Maß, d.h.,
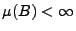 gilt für
jede beschränkte Borel-Menge
gilt für
jede beschränkte Borel-Menge
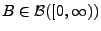 . Das
zufällige Zählmaß
. Das
zufällige Zählmaß
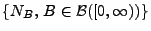 wird
(inhomogenes) Poissonsches Zählmaß mit dem Intensitätsmaß
wird
(inhomogenes) Poissonsches Zählmaß mit dem Intensitätsmaß
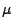 genannt, wenn
genannt, wenn
- die Zufallsvariablen
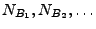 unabhängig sind für
beliebige beschränkte und paarweise disjunkte Borel-Mengen
unabhängig sind für
beliebige beschränkte und paarweise disjunkte Borel-Mengen
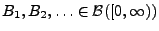 und
und
-
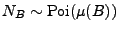 für jedes beschränkte
für jedes beschränkte
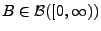 gilt.
gilt.
Man kann sogar noch einen Schritt weiter gehen und sogenannte
doppelt-stochastische Poisson-Prozesse betrachten, die in der
Literatur auch Cox-Prozesse genannt werden.
- Definition
 Sei
Sei
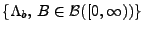 ein
beliebiges zufälliges Maß, das mit Wahrscheinlichkeit
ein
beliebiges zufälliges Maß, das mit Wahrscheinlichkeit  lokal-endlich ist.
lokal-endlich ist.
Ein wichtiger Spezialfall liegt dann vor,
Im folgenden Theorem wird eine Zeittransformation von
homogenen Poisson-Prozessen (mit Intensität 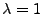 )
betrachtet. Sie liefert einen Algorithmus zur Simulation von
Cox-Prozessen mit vorgegebenem Intensitätsprozess.
)
betrachtet. Sie liefert einen Algorithmus zur Simulation von
Cox-Prozessen mit vorgegebenem Intensitätsprozess.
- Beweis
-
- Wir müssen lediglich zeigen, dass (45) gilt.
- Wegen der vorausgesetzten Unabhängigkeit der Prozesse
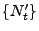 und
und
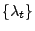 können wir annehmen, dass
der Wahrscheinlichkeitsraum
können wir annehmen, dass
der Wahrscheinlichkeitsraum
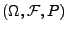 , der beide Prozesse
,,trägt'', die Form
hat, wobei
, der beide Prozesse
,,trägt'', die Form
hat, wobei
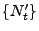 über
über
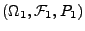 und
und
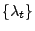 über
über
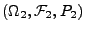 definiert ist.
definiert ist.
- Aus der Definitionsgleichung (47) des Zählprozesses
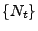 und aus den in Abschnitt 2.2.3 diskutierten
Eigenschaften der bedingten Erwartung ergibt sich, dass
und aus den in Abschnitt 2.2.3 diskutierten
Eigenschaften der bedingten Erwartung ergibt sich, dass
wobei sich die beiden letzten Gleichheiten aus den
Unabhängigkeitseigenschaften der Prozesse
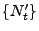 und
und
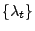 und aus der Darstellungsformel
(40) der regulären bedingten Erwartung für
Funktionale unabhängiger stochastischer Prozesse ergeben.
und aus der Darstellungsformel
(40) der regulären bedingten Erwartung für
Funktionale unabhängiger stochastischer Prozesse ergeben.
- Weil
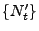 ein homogener Poisson-Prozess mit der
Intensität
ein homogener Poisson-Prozess mit der
Intensität 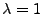 ist, der unabhängig von
ist, der unabhängig von
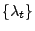 ist, ergibt sich durch die erneute Anwendung der
Darstellungsformel (40), dass für jedes
ist, ergibt sich durch die erneute Anwendung der
Darstellungsformel (40), dass für jedes
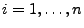
- Hieraus ergibt sich, dass
wobei der letzte Ausdruck mit der rechten Seite von
(45) übereinstimmt.

- Bespiele

- Eine spezielle Klasse von Cox-Prozessen sind die gemischten
Poisson-Prozesse, deren Intensitätsprozess
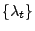 durch
durch
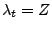 gegeben ist, wobei
gegeben ist, wobei
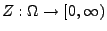 eine
beliebige nichtnegative Zufallsvariable ist.
eine
beliebige nichtnegative Zufallsvariable ist.
- Sei
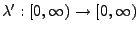 eine periodische (und
deterministische) Funktion mit der Periode
eine periodische (und
deterministische) Funktion mit der Periode  , und sei
, und sei
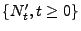 ein (homogener) Poisson-Prozess mit der
Intensität
ein (homogener) Poisson-Prozess mit der
Intensität 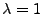 .
.
- Dann wird der Zählprozess
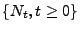 mit
mit
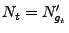
und
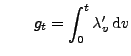
ein periodischer
Poisson-Prozess genannt, der im allgemeinen keine stationären
Zuwächse hat.
- Es ist jedoch möglich, auf die
folgende Weise einen entsprechenden Cox-Prozess mit stationären
Zuwächsen zu konstruieren.




Nächste Seite: Markow-Prozesse mit endlich vielen
Aufwärts: Zählprozesse vom Poisson-Typ
Vorherige Seite: Bedingte Erwartung und bedingte
Inhalt
Ursa Pantle
2005-07-13
![]() mit
mit
![]() und
und
![]() ,
wobei die Zufallsvariablen
,
wobei die Zufallsvariablen
![]() unabhängig und identisch Exp(
unabhängig und identisch Exp(![]() )-verteilt sind, lässt sich
wie folgt weiter verallgemeinern.
)-verteilt sind, lässt sich
wie folgt weiter verallgemeinern.
![]() )
betrachtet. Sie liefert einen Algorithmus zur Simulation von
Cox-Prozessen mit vorgegebenem Intensitätsprozess.
)
betrachtet. Sie liefert einen Algorithmus zur Simulation von
Cox-Prozessen mit vorgegebenem Intensitätsprozess.
![$\displaystyle {P\Bigl(\bigcap_{i=1}^n\{N_{(a_i,b_i]}=k_i\}\Bigr)
=P\Bigl(\bigcap_{i=1}^n\{N_{b_i}-N_{a_i}=k_i\}\Bigr)}$](img551.png)
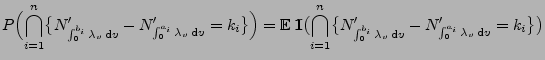
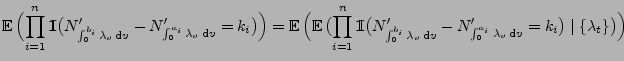
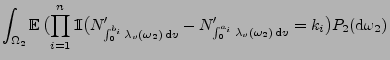
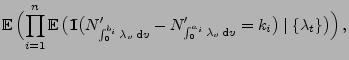
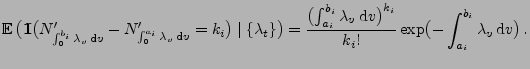
![$\displaystyle P\Bigl(\bigcap_{i=1}^n\{N_{(a_i,b_i]}=k_i\}\Bigr)=
{\mathbb{E}\,}...
...r)^{k_i}}{k_i!} \exp\bigl(- \int_{a_i}^{b_i}\lambda_v\,{\rm d}v\bigr)\Bigr)\,,
$](img559.png)