



Nächste Seite: Übergangsintensitäten
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Markow-Prozesse mit endlich vielen
Inhalt
Anfangsverteilung und
Übergangsfunktion
Um den Begriff eines Markow-Prozesses
 mit
stetiger Zeit und mit Werten in der Menge
mit
stetiger Zeit und mit Werten in der Menge
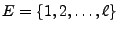 einzuführen, betrachten wir erneut
einzuführen, betrachten wir erneut
- einen Vektor von Wahrscheinlichkeiten
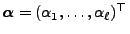 mit
mit
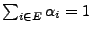 sowie
sowie
- eine Familie von stochastischen Matrizen
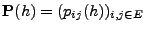 für jedes
für jedes 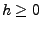 .
.
- Beachte
-
- Im Unterschied zu Markow-Prozessen mit diskreter Zeit muss nun
vorausgesetzt werden, dass
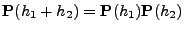 |
(8) |
für beliebige
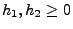 gilt, wobei die Matrix-Identität
(8) wiederum die Gleichung von
Chapman-Kolmogorow genannt wird.
gilt, wobei die Matrix-Identität
(8) wiederum die Gleichung von
Chapman-Kolmogorow genannt wird.
- Außerdem wird vorausgesetzt, dass
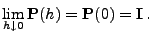 |
(9) |
- Es ist nicht schwierig zu zeigen, dass die Matrix-Funktion
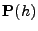 dann gleichmäßig stetig in
dann gleichmäßig stetig in 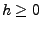 ist.
ist.
- Definition

- Eine Familie von stochastischen Matrizen
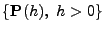 , die
den Bedingungen (8) und (9)
genügt, wird Matrix-Übergangsfunktion bzw. kurz Übergangsfunktion genannt.
, die
den Bedingungen (8) und (9)
genügt, wird Matrix-Übergangsfunktion bzw. kurz Übergangsfunktion genannt.
- Ein stochastischer Prozess
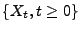 mit Werten in
mit Werten in
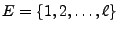 heißt homogener Markow-Prozess,
wenn es eine Übergangsfunktion
heißt homogener Markow-Prozess,
wenn es eine Übergangsfunktion
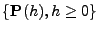 und eine
Wahrscheinlichkeitsfunktion
und eine
Wahrscheinlichkeitsfunktion
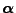 über
über 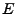 gibt, so dass
gibt, so dass
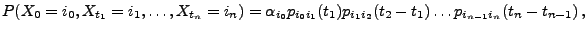 |
(10) |
für beliebige
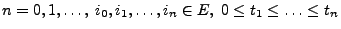 gilt.
gilt.
- Die Wahrscheinlichkeitsfunktion
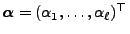 heißt Anfangsverteilung des Markow-Prozesses
heißt Anfangsverteilung des Markow-Prozesses  .
.
Ähnlich wie für Markow-Ketten in Theorem MK-2.1 lässt sich die
folgende Charakterisierung von homogenen Markow-Prozessen mit
stetiger Zeit herleiten, die wir deshalb ohne Beweis angeben. Das
Adjektiv ,,homogen'' werden wir im Folgenden der Kürze wegen
weglassen.
Theorem 2.14
Ein stochastischer Prozess

mit Werten in
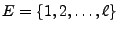
ist genau dann ein Markow-Prozess, wenn
es eine Übergangsfunktion
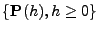
gibt, so dass
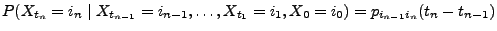 |
(11) |
für diejenigen
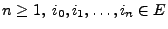
und
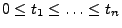
, für die
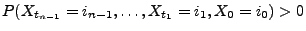
gilt.
Analog zu Korollar MK-2.1 gilt auch für Markow-Prozesse mit
stetiger Zeit die folgende bedingte Unabhängigkeitseigenschaft.




Nächste Seite: Übergangsintensitäten
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Markow-Prozesse mit endlich vielen
Inhalt
Ursa Pantle
2005-07-13
![]() mit
stetiger Zeit und mit Werten in der Menge
mit
stetiger Zeit und mit Werten in der Menge
![]() einzuführen, betrachten wir erneut
einzuführen, betrachten wir erneut