Nächste Seite: Kolmogorowsche Differentialgleichungen
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Anfangsverteilung und Übergangsfunktion
Inhalt
Übergangsintensitäten
Mit der Schreibweise
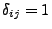 , falls
, falls 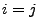 , und
, und
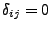 , falls
, falls 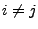 , können wir die folgende
grundlegende Differenzierbarkeitseigenschaft von
Übergangsfunktionen formulieren.
, können wir die folgende
grundlegende Differenzierbarkeitseigenschaft von
Übergangsfunktionen formulieren.
Theorem 2.15
Sei
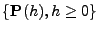
eine Übergangsfunktion. Dann existieren
die (endlichen) Grenzwerte
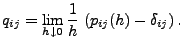 |
(13) |
- Beweis
-
- Weil in der Behauptung von Theorem 2.15 die
Anfangsverteilung nicht näher spezifiziert wird, können wir ohne
Einschränkung der Allgemeinheit annehmen,
- dass
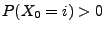 für jedes
für jedes 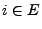 gilt,
gilt,
- wobei wir die Gültigkeit von (13) zuerst für
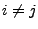 zeigen.
zeigen.
- Dabei setzen wir
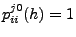 und
und
- Aus (8) ergibt sich dann, dass
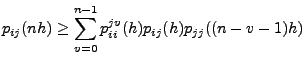 |
(14) |
und
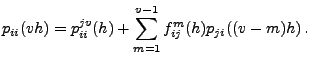 |
(15) |
- Weil
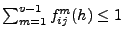 gilt, ergibt sich aus
(15) die Ungleichung
gilt, ergibt sich aus
(15) die Ungleichung
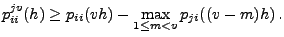 |
(16) |
- Mit Hilfe von (9) erhalten wir nun, dass es für
beliebige
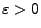 und
und 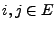 mit
mit 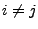 ein
ein 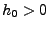 gibt, so dass
gibt, so dass
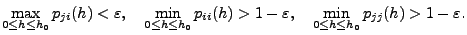 |
(17) |
- Für
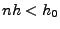 und
und 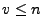 ergibt sich somit aus
(16), dass
ergibt sich somit aus
(16), dass
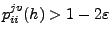 .
.
- Wenn man dies in (14) einsetzt, dann ergibt sich die
Ungleichung
bzw.
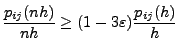 |
(18) |
für 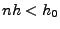 .
.
- Mit der Schreibweise
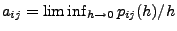 ergibt
dies, dass
ergibt
dies, dass
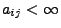 .
.
- Somit gilt
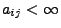 , und es genügt zu zeigen, dass
, und es genügt zu zeigen, dass
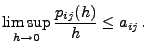 |
(19) |
- Damit ist die Existenz der Grenzwerte
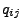 in
(13) für
in
(13) für 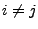 bewiesen.
bewiesen.
- Weil der Zustandsraum
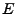 endlich ist und
endlich ist und
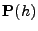 eine
stochastische Matrix ist, gilt außerdem
eine
stochastische Matrix ist, gilt außerdem
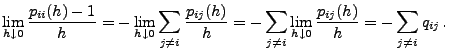 |
(20) |
Damit ist die Behauptung vollständig bewiesen.

- Definition
 Die Matrix
Die Matrix
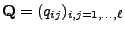 heißt Intensitätsmatrix
heißt Intensitätsmatrix des Markow-Prozesses
des Markow-Prozesses  .
Die Eintragungen
.
Die Eintragungen 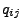 von
von
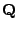 werden Übergangsintensitäten genannt.
werden Übergangsintensitäten genannt.
Korollar 2.2
Für beliebige
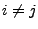
gilt
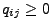
und
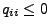
.
Außerdem gilt
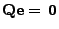
bzw. (äquivalent hierzu)
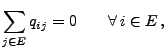 |
(21) |
wobei
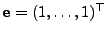
bzw.
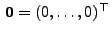
den
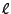
-dimensionalen Einheits- bzw. Nullvektor bezeichnet.
- Beweis
-
- Aus der Definition (13) der Übergangsintensitäten
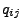 ergibt sich unmittelbar, dass
ergibt sich unmittelbar, dass
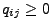 und
und
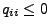 für beliebige
für beliebige 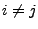 gilt.
gilt.
- Die Behauptung (21) folgt somit aus
(20).

- Beachte
-
- Die Definition von Markow-Prozessen und ihre Charakterisierung in
Theorem 2.14 lassen sich völlig analog für
Markow-Prozesse mit einem (abzählbar) unendlichen Zustandsraum
formulieren, beispielsweise für
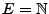 .
.
- Die in Theorem 2.15 hergeleitete
Differenzierbarkeitseigenschaft der Übergangsfunktion
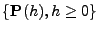 bleibt ebenfalls (in einer etwas modifizierten Form)
gültig.
bleibt ebenfalls (in einer etwas modifizierten Form)
gültig.
- Im Beweis von Theorem 2.15 wird nämlich die
Endlichkeit des Zustandsraumes
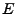 nicht benötigt, um die
Existenz und Endlichkeit der Übergangsintensitäten
nicht benötigt, um die
Existenz und Endlichkeit der Übergangsintensitäten 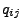 für
für
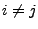 zu zeigen.
zu zeigen.
- Außerdem kann man auch zeigen, dass die Grenzwerte
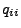 in
(13) existieren, wenn der Zustandsraum
in
(13) existieren, wenn der Zustandsraum 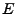 unendlich ist; sie müssen aber nicht notwendig endlich sein.
unendlich ist; sie müssen aber nicht notwendig endlich sein.
- Im allgemeinen kann man dann (anstelle von (20)) nur
zeigen, dass
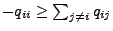 für jedes
für jedes 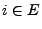 gilt, wobei der Fall der Gleichheit von besonderer Bedeutung ist.
gilt, wobei der Fall der Gleichheit von besonderer Bedeutung ist.
- Definition
 Wenn der Zustandsraum
Wenn der Zustandsraum 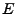 unendlich ist, dann
sagt man, dass die Übergangsfunktion
unendlich ist, dann
sagt man, dass die Übergangsfunktion
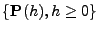 konservativ ist, falls
konservativ ist, falls
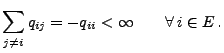 |
(22) |
- Beachte
 Die meisten Ergebnisse, die wir in dieser Vorlesung für
Markow-Prozesse mit endlichem Zustandsraum herleiten, bleiben für
konservative Übergangsfunktionen in (abzählbar) unendlichen
Zustandsräumen gültig. Die Beweise sind dann jedoch oft
wesentlich aufwändiger.
Die meisten Ergebnisse, die wir in dieser Vorlesung für
Markow-Prozesse mit endlichem Zustandsraum herleiten, bleiben für
konservative Übergangsfunktionen in (abzählbar) unendlichen
Zustandsräumen gültig. Die Beweise sind dann jedoch oft
wesentlich aufwändiger.
- Beispiel

- Man kann sich leicht überlegen, dass jeder stochastische Prozess
 mit Werten in
mit Werten in
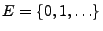 , der
unabhängige und stationäre Zuwächse hat, ein Markow-Prozess ist.
, der
unabhängige und stationäre Zuwächse hat, ein Markow-Prozess ist.
- Insbesondere ist somit der (homogene) Poisson-Prozess mit
Intensität
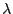 ein Markow-Prozess.
ein Markow-Prozess.
- In diesem Fall gilt
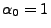 und
und
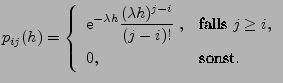 |
(23) |
- Hieraus folgt, dass




Nächste Seite: Kolmogorowsche Differentialgleichungen
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Anfangsverteilung und Übergangsfunktion
Inhalt
Ursa Pantle
2005-07-13
![]() , falls
, falls ![]() , und
, und
![]() , falls
, falls ![]() , können wir die folgende
grundlegende Differenzierbarkeitseigenschaft von
Übergangsfunktionen formulieren.
, können wir die folgende
grundlegende Differenzierbarkeitseigenschaft von
Übergangsfunktionen formulieren.