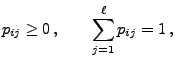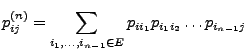Nächste Seite: Anfangsverteilung und Übergangsfunktion
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Poissonsche Zählmaße; Cox-Prozesse; Simluationsalgorithmus
Inhalt
Markow-Prozesse mit endlich vielen
Zuständen
Wir beginnen mit einem kurzen Rückblick auf Markow-Prozesse mit
diskreter Zeit, die in der Literatur Markow-Ketten genannt
werden und die beispielsweise in der Vorlesung ,,Markow-Ketten
und Monte-Carlo-Simulation'' im SS 2003 ausführlich behandelt
wurden.
- Das stochastische Modell der zeitdiskreten Markow-Ketten (mit
endlich vielen Zuständen) besteht aus den drei Komponenten:
Zustandsraum, Anfangsverteilung und Übergangsmatrix.
- Für jede Menge
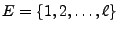 , für jeden Vektor
, für jeden Vektor
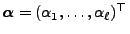 bzw. jede Matrix
bzw. jede Matrix
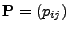 , die den Bedingungen (1) und
(2) genügen, kann nun der Begriff der zugehörigen
Markow-Kette wie folgt eingeführt werden.
, die den Bedingungen (1) und
(2) genügen, kann nun der Begriff der zugehörigen
Markow-Kette wie folgt eingeführt werden.
- Definition
-
- Beachte
-
Unterabschnitte




Nächste Seite: Anfangsverteilung und Übergangsfunktion
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Poissonsche Zählmaße; Cox-Prozesse; Simluationsalgorithmus
Inhalt
Ursa Pantle
2005-07-13
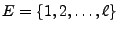 identifiziert
werden kann, wobei
identifiziert
werden kann, wobei
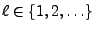 eine beliebige, jedoch
fest vorgegebene natürliche Zahl ist.
eine beliebige, jedoch
fest vorgegebene natürliche Zahl ist.
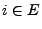 sei
sei 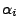 die Wahrscheinlichkeit, dass
sich das betrachtete System zum ,,Zeitpunkt''
die Wahrscheinlichkeit, dass
sich das betrachtete System zum ,,Zeitpunkt'' 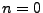 im Zustand
im Zustand 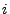 befindet, wobei
befindet, wobei
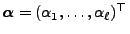 der (Einzel-)
Wahrscheinlichkeiten
der (Einzel-)
Wahrscheinlichkeiten
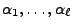 bildet die Anfangsverteilung der Markow-Kette.
bildet die Anfangsverteilung der Markow-Kette.
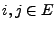 die (bedingte)
Wahrscheinlichkeit
die (bedingte)
Wahrscheinlichkeit
![$ p_{ij}\in[0,1]$](img582.png) , dass das betrachtete System
in einem Schritt aus dem Zustand
, dass das betrachtete System
in einem Schritt aus dem Zustand 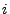 in den Zustand
in den Zustand 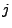 übergeht.
übergeht.
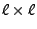 Matrix
Matrix
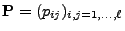 der Übergangswahrscheinlichkeiten
der Übergangswahrscheinlichkeiten 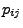 mit
mit
![$\displaystyle \alpha_i\in[0,1]\,,\qquad\sum\limits_{i=1}^\ell \alpha_i=1$](img578.png)