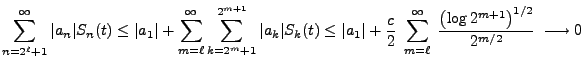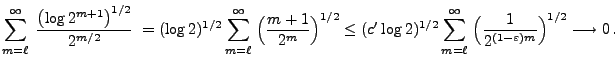Nächste Seite: Eigenschaften normalverteilter Zufallsvariablen
Aufwärts: Wiener-Prozess
Vorherige Seite: Wiener-Prozess
Inhalt
Vollständige Orthonormalsysteme im 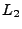 ; Haar-Funktionen
und Schauder-Funktionen
; Haar-Funktionen
und Schauder-Funktionen
Wir betrachten zunächst den Fall, dass ![$ I=[0,1]$](img919.png) das
Einheitsintervall ist. Dabei benötigen wir zur Konstruktion von
Wiener-Prozessen in
das
Einheitsintervall ist. Dabei benötigen wir zur Konstruktion von
Wiener-Prozessen in ![$ [0,1]$](img566.png) einige analytische Hilfsmittel.
einige analytische Hilfsmittel.
- Insbesondere betrachten wir den Hilbert-Raum
![$ L_2=L_2([0,1])$](img920.png)
- aller auf dem Einheitsintervall
![$ I=[0,1]$](img919.png) definierten
(Borel-messbaren) Funktionen
definierten
(Borel-messbaren) Funktionen
![$ f:[0,1]\to\mathbb{R}$](img921.png) , die bezüglich des
Lebesgue-Maßes quadratisch integrierbar sind, d.h., für die
, die bezüglich des
Lebesgue-Maßes quadratisch integrierbar sind, d.h., für die
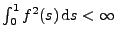 gilt.
gilt.
- Für beliebige
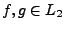 sei
sei
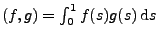 das zugehörige Skalarprodukt.
das zugehörige Skalarprodukt.
- Eine Folge
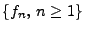 von Funktionen
von Funktionen
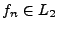 wird
ein vollständiges Orthonormalsystem in
wird
ein vollständiges Orthonormalsystem in 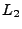 genannt,
genannt,
- wenn
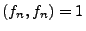 und
und
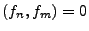 für beliebige
für beliebige 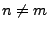 und
und
- wenn für jedes
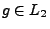 die Gültigkeit von
die Gültigkeit von 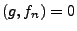 für jedes
für jedes
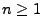 impliziert, dass
impliziert, dass 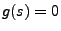 für fast jedes
für fast jedes ![$ s\in[0,1]$](img933.png) .
.
Die Konstruktion von Wiener-Prozessen in ![$ I=[0,1]$](img919.png) beruht auf der
Idee,
beruht auf der
Idee,
- Definition
 Die durch den Ansatz
Die durch den Ansatz
für
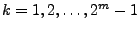 und
und
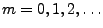 gegebenen Funktionen
gegebenen Funktionen
![$ H_n:[0,1]\to\mathbb{R}$](img946.png) heißen Haar-Funktionen.
heißen Haar-Funktionen.
- Beweis
-
- Unmittelbar aus der Definition der Haar-Funktionen folgt, dass
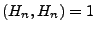 und
und
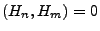 für beliebige
für beliebige 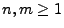 mit
mit
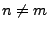 gilt.
gilt.
- Außerdem kann man leicht zeigen, dass das Orthonormalsystem
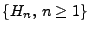 vollständig in
vollständig in 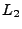 ist.
ist.
- Die Gültigkeit von (5) ergibt sich aus der
Vollständigkeit des Orthonormalsystems
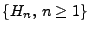 , vgl.
beispielsweise Satz 5.3.6 in W. Arendt (2002) Funktionalanalysis
(Vorlesungskript, Universität Ulm) bzw. Satz V.4.9 in D. Werner
(1997) Funktionalanalysis (Springer, Berlin).
, vgl.
beispielsweise Satz 5.3.6 in W. Arendt (2002) Funktionalanalysis
(Vorlesungskript, Universität Ulm) bzw. Satz V.4.9 in D. Werner
(1997) Funktionalanalysis (Springer, Berlin).
- Beweis
-




Nächste Seite: Eigenschaften normalverteilter Zufallsvariablen
Aufwärts: Wiener-Prozess
Vorherige Seite: Wiener-Prozess
Inhalt
Ursa Pantle
2005-07-13
![]() das
Einheitsintervall ist. Dabei benötigen wir zur Konstruktion von
Wiener-Prozessen in
das
Einheitsintervall ist. Dabei benötigen wir zur Konstruktion von
Wiener-Prozessen in ![]() einige analytische Hilfsmittel.
einige analytische Hilfsmittel.
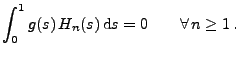
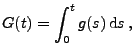
![$\displaystyle S_{2^m+k}(t)\le S_{2^m+k}\Bigl(\frac{2k-1}{2^{m+1}}\Bigr)=
2^{m/2}\;\frac{1}{2^{m+1}}\;=\;\frac{1}{2}\;2^{-m/2}\qquad\forall\,t\in[0,1]\,.
$](img976.png)