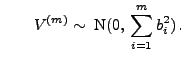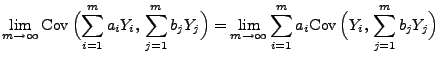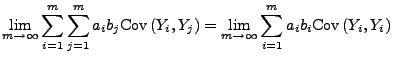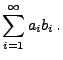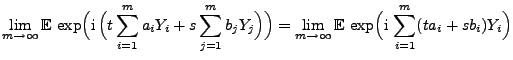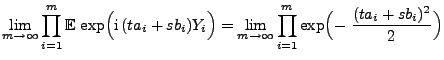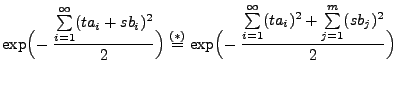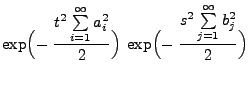Bei der Konstruktion von Wiener-Prozessen benötigen wir noch die
folgenden Eigenschaften von normalverteilten Zufallsvariablen.
Lemma 2.7

Sei
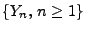
eine Folge von (nicht notwendig
unabhängigen) N
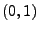
-verteilten Zufallsvariablen über
einunddemselben Wahrscheinlichkeitsraum
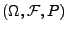
. Dann
gilt mit Wahrscheinlichkeit

, dass
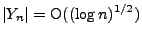 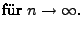 |
(8) |
Lemma 2.8

Die Zufallsvariablen
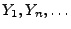
seien unabhängig und
N
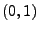
-normalverteilt. Außerdem seien
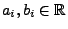
beliebige Konstanten, so dass für jedes
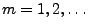
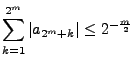 und und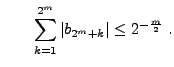 |
(10) |
Dann existieren die Grenzwerte
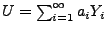
und
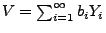
mit Wahrscheinlichkeit

, und es
gilt
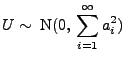 und und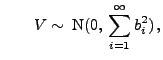 |
(11) |
wobei
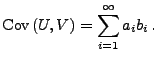 |
(12) |
Außerdem sind die Zufallsvariablen
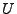
und
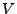
sind genau dann
unabhängig, wenn
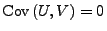
.
![$\displaystyle \int_x^\infty \;\frac{1}{y^2}\;{\rm e}^{-y^2/2}\,{\rm d}y=
\Bigl[...
...rm e}^{-y^2/2}\Bigr]_x^\infty\;-\;
\int_x^\infty \; {\rm e}^{-y^2/2}\,{\rm d}y
$](img990.png)
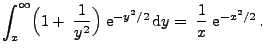
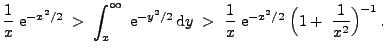
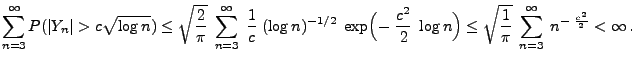
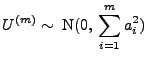 und
und