



Nächste Seite: Vollständige Orthonormalsysteme im ;
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Stationäre Anfangsverteilungen
Inhalt
Wiener-Prozess
Der Wiener-Prozess, der in der Literatur auch Brownsche
Bewegung genannt wird, ist ein weiteres grundlegendes Modell in
der Theorie stochastischer Prozesse. Dabei nehmen wir für die
Indexmenge 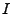 an, dass entweder
an, dass entweder ![$ I=[0,b]$](img910.png) für eine (endliche)
Zahl
für eine (endliche)
Zahl
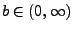 oder
oder
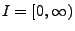 gilt.
gilt.
- Definition
 Ein stochastischer Prozess
Ein stochastischer Prozess
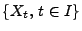 über einem (im
allgemeinen nicht näher spezifizierten) Wahrscheinlichkeitsraum
über einem (im
allgemeinen nicht näher spezifizierten) Wahrscheinlichkeitsraum
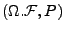 heisst Wiener-Prozess (im Zeitintervall
heisst Wiener-Prozess (im Zeitintervall
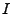 ), wenn
), wenn
-
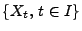 unabhängige Zuwächse hat,
unabhängige Zuwächse hat,
-
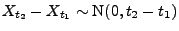 für beliebige
für beliebige
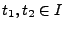 mit
mit 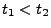 ,
,
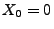 ,
,
- die Trajektorie
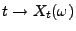 ,
, 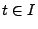 , für jedes
, für jedes
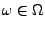 eine stetige Funktion ist.
eine stetige Funktion ist.
- Beachte

- Aus dem Existenzsatz von Kolmogorow, d.h. aus
Theorem 1.1, folgt, dass es einen
Wahrscheinlichkeitsraum und einen stochastischen Prozess
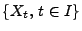 über diesem Wahrscheinlichkeitsraum gibt, so
dass die ersten drei Bedingungen in der Definition des
Wiener-Prozesses erfüllt sind.
über diesem Wahrscheinlichkeitsraum gibt, so
dass die ersten drei Bedingungen in der Definition des
Wiener-Prozesses erfüllt sind.
- Aus dem Stetigkeitssatz von Kolmogorow, d.h. aus
Theorem 1.3, folgt außerdem, dass zu jedem Prozess
 , der den ersten drei Bedingungen in der
Definition des Wiener-Prozesses genügt, eine stetige Modifikation
existiert.
, der den ersten drei Bedingungen in der
Definition des Wiener-Prozesses genügt, eine stetige Modifikation
existiert.
- Weniger offensichtlich ist, ob bzw. wie man einen solchen Prozess
(mit unabhängigen und normalverteilten Zuwächsen) explizit
konstruieren kann, dessen Trajektorien stetige Funktionen sind.
- In den drei folgenden Abschnitten erläutern wir eine Methode zur
Konstruktion von Wiener-Prozessen (mit stetigen Trajektorien),
die gleichzeitig zu einem Algorithmus zur Simulation von
Wiener-Prozessen führt.
Unterabschnitte




Nächste Seite: Vollständige Orthonormalsysteme im ;
Aufwärts: Prozesse mit stückweise konstanten
Vorherige Seite: Stationäre Anfangsverteilungen
Inhalt
Ursa Pantle
2005-07-13
![]() an, dass entweder
an, dass entweder ![]() für eine (endliche)
Zahl
für eine (endliche)
Zahl
![]() oder
oder
![]() gilt.
gilt.