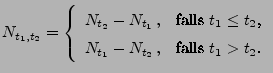Nächste Seite: Allgemeines Konstruktionsprinzip für Zählprozesse
Aufwärts: Zählprozesse im
Vorherige Seite: Zählprozesse im
Inhalt
Homogener Poisson-Prozess
In diesem Abschnitt betrachten wir zunächst den Fall, dass die
,,Zwischenankunftszeiten''
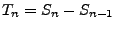 zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
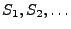
- eine Folge
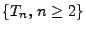 von
unabhängigen und identisch verteilten Zufalllsvariablen bilden mit
von
unabhängigen und identisch verteilten Zufalllsvariablen bilden mit
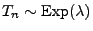 für ein
für ein 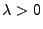 .
.
- Außerdem sei
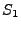 unabhängig von
unabhängig von
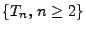 , und es gelte
, und es gelte
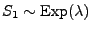 .
.
- Dann ist der Zählprozess
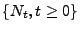 mit
mit
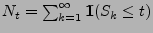 ein (homogener)
Poisson-Prozess in
ein (homogener)
Poisson-Prozess in
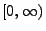 mit der Intensität
mit der Intensität 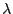 ;
vgl. Abschnitt 2.2.1.
;
vgl. Abschnitt 2.2.1.
Wir zeigen, wie der Zählprozess
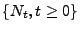 auf einfache
Weise zu einem Zählprozess
auf einfache
Weise zu einem Zählprozess
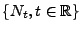 auf der gesamten
reellen Achse
auf der gesamten
reellen Achse
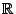 fortgesetzt werden kann, so dass
fortgesetzt werden kann, so dass
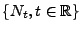 stationäre und unabhängige (poissonverteilte) Zuwächse hat.
stationäre und unabhängige (poissonverteilte) Zuwächse hat.
Theorem 4.2

Sei
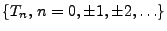
eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen mit
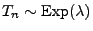
für ein
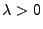
. Außerdem sei
![$\displaystyle S_n=\left\{\begin{array}{rl} \sum_{k=1}^n T_k & \mbox{für $n\ge 1$,}\\ [3\jot] -\sum_{k=n}^0 T_k & \mbox{für $n\le 0$.} \end{array}\right.$](img2033.png) |
(3) |
Dann hat der in
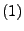
gegebene Zählprozess
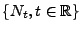
stationäre und unabhängige Zuwächse, wobei
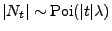
für jedes
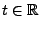
.
- Beweis
-
- Beachte
-
Das folgende Resultat zeigt,
- wie sich das in (4) betrachtete Modell eines
(inhomogenen) Zählprozesses vom Poisson-Typ durch Grenzübergang
aus einer bedingten Version des in (3)
eingeführten Modells des homogenen Poisson-Prozesses ergibt.
- Dabei wird das letztere Modell unter der Bedingung betrachtet,
dass in einer (kleinen)
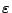 -Umgebung des Nullpunktes
ein Ereigniszeitpunkt liegt.
-Umgebung des Nullpunktes
ein Ereigniszeitpunkt liegt.
Hierfür benötigen wir die folgenden Bezeichnungen. Sei
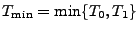 , und für beliebige
, und für beliebige
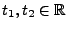 sei
sei
- Beweis
-




Nächste Seite: Allgemeines Konstruktionsprinzip für Zählprozesse
Aufwärts: Zählprozesse im
Vorherige Seite: Zählprozesse im
Inhalt
Ursa Pantle
2005-07-13
![]() zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
zwischen den
aufeinanderfolgenden Ereigniszeitpunkten
![]()
![]() auf einfache
Weise zu einem Zählprozess
auf einfache
Weise zu einem Zählprozess
![]() auf der gesamten
reellen Achse
auf der gesamten
reellen Achse
![]() fortgesetzt werden kann, so dass
fortgesetzt werden kann, so dass
![]() stationäre und unabhängige (poissonverteilte) Zuwächse hat.
stationäre und unabhängige (poissonverteilte) Zuwächse hat.
![]() , und für beliebige
, und für beliebige
![]() sei
sei