



Nächste Seite: Homogener Poisson-Prozess
Aufwärts: Stochastische Prozesse und Felder
Vorherige Seite: Stochastische Prozesse und Felder
Inhalt
Zählprozesse im
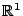
Wir modifizieren das in Abschnitt ![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) eingeführte
Konzept von Zählprozessen
eingeführte
Konzept von Zählprozessen
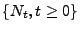 dahingehend, dass wir
Zählprozesse ,,mit Vergangenheit'' betrachten, d.h., die in
Abschnitt
dahingehend, dass wir
Zählprozesse ,,mit Vergangenheit'' betrachten, d.h., die in
Abschnitt ![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) betrachteten Ereigniszeitpunkte
betrachteten Ereigniszeitpunkte 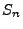 liegen jetzt nicht nur in
liegen jetzt nicht nur in
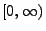 , sondern sie sind auf der
gesamten reellen Achse
, sondern sie sind auf der
gesamten reellen Achse
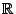 verteilt.
verteilt.
- Definition
-
- Beachte
-
- Definition
-
- Man sagt, dass der Zählprozess
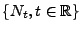 stationäre Zuwächse hat, wenn für beliebige
stationäre Zuwächse hat, wenn für beliebige
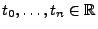 mit
mit
 die Verteilungen
der Zufallsvektoren
die Verteilungen
der Zufallsvektoren
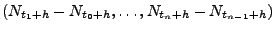 nicht von
nicht von 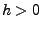 abhängen.
abhängen.
- Außerdem sagt man, dass
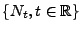 ein Prozess
mit unabhängigen Zuwächsen ist, wenn die Zufallsvariablen
ein Prozess
mit unabhängigen Zuwächsen ist, wenn die Zufallsvariablen
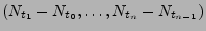 für beliebige
für beliebige
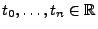 mit
mit
 unabhängig sind.
unabhängig sind.
- Das zufällige Zählmaß
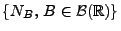 heißt stationär, wenn für beliebige
heißt stationär, wenn für beliebige
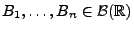 und
und
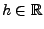 die Verteilungen der Zufallsvektoren
die Verteilungen der Zufallsvektoren
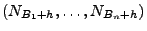 nicht von
nicht von 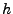 abhängen.
abhängen.
Theorem 4.1

Sei
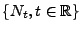
ein Zählprozess über
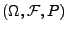
,
und das Zählmaß
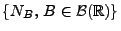
sei gegeben durch
. Der Prozess
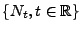
hat genau
dann stationäre Zuwächse, wenn
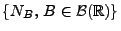
stationär ist.
- Beweis
-
Unterabschnitte




Nächste Seite: Homogener Poisson-Prozess
Aufwärts: Stochastische Prozesse und Felder
Vorherige Seite: Stochastische Prozesse und Felder
Inhalt
Ursa Pantle
2005-07-13
![]() eingeführte
Konzept von Zählprozessen
eingeführte
Konzept von Zählprozessen
![]() dahingehend, dass wir
Zählprozesse ,,mit Vergangenheit'' betrachten, d.h., die in
Abschnitt
dahingehend, dass wir
Zählprozesse ,,mit Vergangenheit'' betrachten, d.h., die in
Abschnitt ![]() betrachteten Ereigniszeitpunkte
betrachteten Ereigniszeitpunkte ![]() liegen jetzt nicht nur in
liegen jetzt nicht nur in
![]() , sondern sie sind auf der
gesamten reellen Achse
, sondern sie sind auf der
gesamten reellen Achse
![]() verteilt.
verteilt.