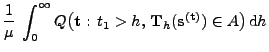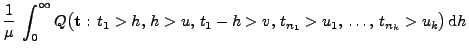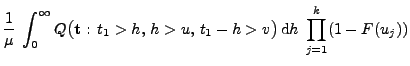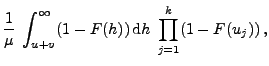Nächste Seite: Semi-Markowsche Zählprozesse; Simulationsalgorithmus
Aufwärts: Zählprozesse im
Vorherige Seite: Allgemeines Konstruktionsprinzip für Zählprozesse
Inhalt
Erneuerungsprozesse mit stationären Zuwächsen
Wir setzen nun voraus, dass 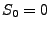 und dass die
Zwischenankunftszeiten
und dass die
Zwischenankunftszeiten
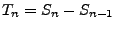 eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen mit einer
beliebigen Verteilungsfunktion
eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen mit einer
beliebigen Verteilungsfunktion 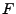 bilden.
bilden.
- Beachte
-
- Wenn die Zwischenankunftszeiten
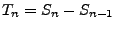 eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen bilden,
dann sagt man, dass der in (1) gegebene
stochastische Prozess
eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen bilden,
dann sagt man, dass der in (1) gegebene
stochastische Prozess
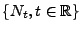 ein gewöhnlicher
Erneuerungszählprozess bzw. kurz ein Erneuerungsprozess
ist, wobei
ein gewöhnlicher
Erneuerungszählprozess bzw. kurz ein Erneuerungsprozess
ist, wobei 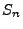 der
der 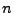 -te Erneuerungszeitpunkt heißt.
-te Erneuerungszeitpunkt heißt.
- Außerdem sagt man, dass der in
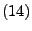 gegebene
Zählprozess
gegebene
Zählprozess
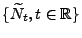 mit stationären Zuwächsen
ein verzögerter Erneuerungsprozess ist.
mit stationären Zuwächsen
ein verzögerter Erneuerungsprozess ist.
- Beweis
-




Nächste Seite: Semi-Markowsche Zählprozesse; Simulationsalgorithmus
Aufwärts: Zählprozesse im
Vorherige Seite: Allgemeines Konstruktionsprinzip für Zählprozesse
Inhalt
Ursa Pantle
2005-07-13
![]() und dass die
Zwischenankunftszeiten
und dass die
Zwischenankunftszeiten
![]() eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen mit einer
beliebigen Verteilungsfunktion
eine Folge von
unabhängigen und identisch verteilten Zufallsvariablen mit einer
beliebigen Verteilungsfunktion ![]() bilden.
bilden.