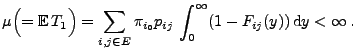Nächste Seite: Poissonsche Zählmaße im
Aufwärts: Zählprozesse im
Vorherige Seite: Erneuerungsprozesse mit stationären Zuwächsen
Inhalt
Semi-Markowsche Zählprozesse; Simulationsalgorithmus
Eine weitere Klasse von Zählprozessen in
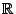 mit stationären
Zuwächsen ergibt sich, wenn das in Theorem 4.4
betrachtete
mit stationären
Zuwächsen ergibt sich, wenn das in Theorem 4.4
betrachtete
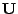 -invariante Wahrscheinlichkeitsmaß
-invariante Wahrscheinlichkeitsmaß 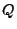 über
über
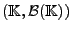 die folgende (verallgemeinerte)
Produktdarstellung besitzt. Dabei verwenden wir einige
grundlegende Begriffe aus der Theorie der zeitdiskreten
Markow-Ketten, vgl. das Skript zur Vorlesung ,,Markow-Ketten und
Monte-Carlo-Simulation'' im SS 2003.
die folgende (verallgemeinerte)
Produktdarstellung besitzt. Dabei verwenden wir einige
grundlegende Begriffe aus der Theorie der zeitdiskreten
Markow-Ketten, vgl. das Skript zur Vorlesung ,,Markow-Ketten und
Monte-Carlo-Simulation'' im SS 2003.
Der Beweis von Theorem 4.6 verläuft ähnlich
wie der Beweis von Theorem 4.4. Er wird deshalb
weggelassen.
- Definition
-
- Wenn die Verteilung
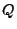 der Zwischenankunftszeiten
der Zwischenankunftszeiten
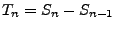 durch (18) gegeben ist, dann sagt
man,
durch (18) gegeben ist, dann sagt
man,
- dass der in (1) gegebene stochastische Prozess
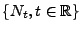 ein semi-Markowscher Zählprozess ist.
ein semi-Markowscher Zählprozess ist.
- In diesem Fall wird der in
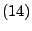 gegebene
Zählprozess
gegebene
Zählprozess
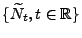 ein verzögerter
semi-Markowscher Zählprozess (mit stationären Zuwächsen)
genannt.
ein verzögerter
semi-Markowscher Zählprozess (mit stationären Zuwächsen)
genannt.
- Für
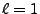 ergeben sich die in Abschnitt 4.1.3
betrachteten Erneuerungprozesse als Spezialfall.
ergeben sich die in Abschnitt 4.1.3
betrachteten Erneuerungprozesse als Spezialfall.
- Beachte
-




Nächste Seite: Poissonsche Zählmaße im
Aufwärts: Zählprozesse im
Vorherige Seite: Erneuerungsprozesse mit stationären Zuwächsen
Inhalt
Ursa Pantle
2005-07-13
![]() mit stationären
Zuwächsen ergibt sich, wenn das in Theorem 4.4
betrachtete
mit stationären
Zuwächsen ergibt sich, wenn das in Theorem 4.4
betrachtete
![]() -invariante Wahrscheinlichkeitsmaß
-invariante Wahrscheinlichkeitsmaß ![]() über
über
![]() die folgende (verallgemeinerte)
Produktdarstellung besitzt. Dabei verwenden wir einige
grundlegende Begriffe aus der Theorie der zeitdiskreten
Markow-Ketten, vgl. das Skript zur Vorlesung ,,Markow-Ketten und
Monte-Carlo-Simulation'' im SS 2003.
die folgende (verallgemeinerte)
Produktdarstellung besitzt. Dabei verwenden wir einige
grundlegende Begriffe aus der Theorie der zeitdiskreten
Markow-Ketten, vgl. das Skript zur Vorlesung ,,Markow-Ketten und
Monte-Carlo-Simulation'' im SS 2003.