



Nächste Seite: Messbare Indizierung der Atome
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Poissonsche Zählmaße im
Inhalt
Definition und elementare
Eigenschaften
Wir führen nun den Begriff des Poissonschen Zählmaßes im
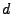 -dimensionalen euklidischen Raum
-dimensionalen euklidischen Raum
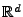 ein.
ein.
- Definition
 Sei
Sei
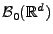 die Familie aller beschränkten Borel-Mengen
in
die Familie aller beschränkten Borel-Mengen
in
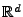 und sei
und sei
![$ \mu:\mathcal{B}(\mathbb{R}^d)\to[0,\infty]$](img2193.png) ein beliebiges
lokal-endliches Maß, d.h.,
ein beliebiges
lokal-endliches Maß, d.h.,
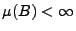 gilt für jedes
gilt für jedes
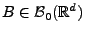 .
.
- Beachte
 Aus Theorem 4.7 ergibt sich, dass die Bedingungen 1
und 2 in der Definition des Poisson-Prozesses durch die folgenden
(scheinbar schwächeren) Bedingungen ersetzt werden können:
Aus Theorem 4.7 ergibt sich, dass die Bedingungen 1
und 2 in der Definition des Poisson-Prozesses durch die folgenden
(scheinbar schwächeren) Bedingungen ersetzt werden können:
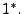
- Die Zufallsvariablen
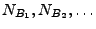 sind unabhängig für
paarweise disjunkte
sind unabhängig für
paarweise disjunkte
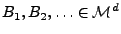 und
und
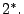
-
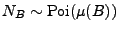 gilt für jedes
gilt für jedes
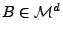 .
.
Wir diskutieren zunächst einige elementare Eigenschaften von
Poisson-Prozessen im
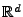 .
.
Theorem 4.8

Sei
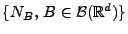
ein Poisson-Prozess mit dem Intensitätsmaß
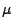
.
Der Beweis von Theorem 4.8 ergibt sich
unmittelbar aus den Bedingungen 1 und 2 in der Definition des
homogenen Poisson-Prozesses.
Mit Hilfe der Theoreme 4.7 und 4.8
lässt sich eine einfache Methode zur Konstruktion von
Poisson-Prozessen mit endlichem Intensitätsmaß herleiten.
Korollar 4.2

Sei
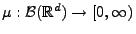
ein beliebiges Maß mit
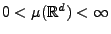
, und
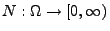
bzw.
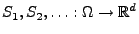
seien
unabhängige Zufallsvariablen mit
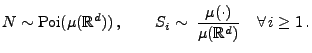 |
(5) |
Dann ist das zufällige Zählmaß
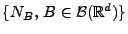
mit
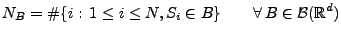 |
(6) |
ein Poisson-Prozess mit dem Intensitätsmaß
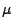
.
- Beweis
-
- Mit der Schreibweise
ergibt sich aus (5) und (6), dass
für jedes
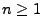 , für beliebige, paarweise disjunkte
, für beliebige, paarweise disjunkte
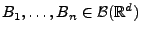 und für
und für
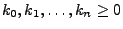 mit
mit
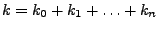 , wobei
, wobei
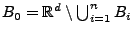 .
.
- Hieraus folgt, dass
- Vergleicht man dieses Ergebnis mit der Formel (3)
in Theorem 4.8, dann erkennt man, dass das in
(6) gegebene zufällige Zählmaß die gleichen
endlich-dimensionalen Verteilungen hat wie ein Poisson-Prozess
mit dem Intensitätsmaß
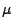 .
.
- Hieraus und aus Theorem 4.7 ergibt sich sich nun die
Behauptung.

- Beachte
-
Das folgende Resultat über die Summation von unabhängigen
Poisson-Prozessen ist ein Analogon der Faltungsstabilität von
Poisson-Verteilungen.
Theorem 4.9
Sei
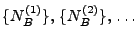
eine Folge
unabhängiger Poisson-Prozesse in
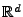
mit den Intensitätsmaßen
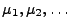
, so dass das Maß
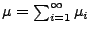
lokal endlich ist. Dann ist das zufällige Zählmaß
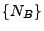
mit
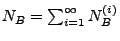
ein Poisson-Prozess mit dem
Intensitätsmaß
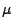
.
- Beweis
-
Wir zeigen nun noch, dass die Einschränkung von Poisson-Prozessen
auf Borelsche Teilmengen des
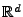 erneut zu Poisson-Prozessen
führt.
erneut zu Poisson-Prozessen
führt.
Theorem 4.10
Sei
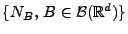
ein Poisson-Prozess mit dem
Intensitätsmaß
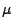
, und sei
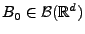
eine beliebige
Borel-Menge. Dann ist das zufällige Zählmaß
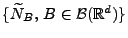
mit
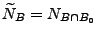
ein
Poisson-Prozess mit dem Intensitätsmaß
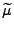
, wobei
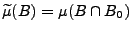
für jedes
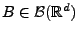
.
- Beweis
-




Nächste Seite: Messbare Indizierung der Atome
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Poissonsche Zählmaße im
Inhalt
Ursa Pantle
2005-07-13
![]() -dimensionalen euklidischen Raum
-dimensionalen euklidischen Raum
![]() ein.
ein.
![]() .
.
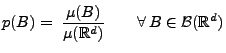
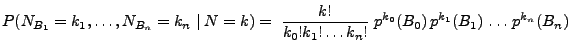
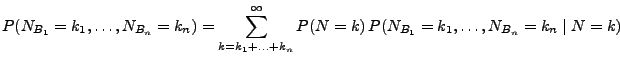
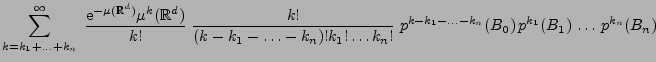
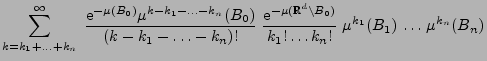
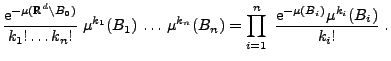
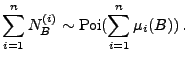
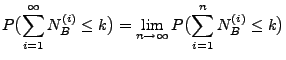
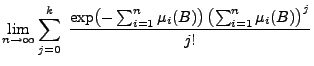
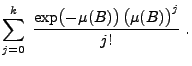
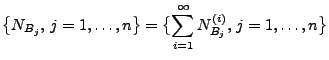
![]() erneut zu Poisson-Prozessen
führt.
erneut zu Poisson-Prozessen
führt.