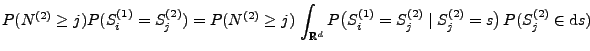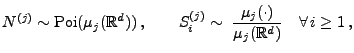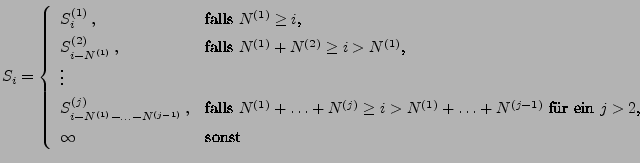Nächste Seite: Simulationsalgorithmus; Akzeptanz- und Verwerfungsmethode
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Definition und elementare Eigenschaften
Inhalt
Messbare Indizierung der Atome
In diesem Abschnitt betrachten wir den Begriff der messbaren
Indizierung der (zufälligen) Atome von Poisson-Prozessen, der
einen konstruktiven Zugang zu Poisson-Prozessen im
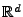 und
somit die mathematische Grundlage von Simulationsalgorithmen
bildet, vgl. auch die Abschnitte 4.2.3 und
4.2.4.
und
somit die mathematische Grundlage von Simulationsalgorithmen
bildet, vgl. auch die Abschnitte 4.2.3 und
4.2.4.
- Beachte
 Man sagt, dass die Folge
Man sagt, dass die Folge
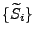 von
Zufallsvektoren
von
Zufallsvektoren
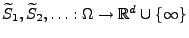 mit
mit
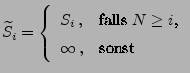 |
(9) |
eine messbare Indizierung der (zufälligen) Atome des in
(6) gegebenen zufälligen Zählmaßes 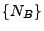 ist.
ist.
Von nun an werden wir stets voraussetzen, dass das Intensitätsmaß
![$ \mu:\mathcal{B}(\mathbb{R}^d)\to[0,\infty]$](img2193.png) diffus ist, d.h., es gelte
diffus ist, d.h., es gelte
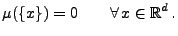 |
(10) |
Der folgende Hilfssatz wird manchmal Disjunktheitstheorem
genannt. Wir nutzen dieses Ergebnis, um zu zeigen, dass man auch
für Poissonsche Zählmaße mit einem beliebigen (diffusen und lokal
endlichen) Intensitätsmaß eine messbare Indizierung der Atome
konstruieren kann.
- Beweis
-
- Beachte
 Aus Lemma 4.1 ergibt sich
insbesondere, dass durch
Aus Lemma 4.1 ergibt sich
insbesondere, dass durch
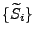 mit
mit
![$\displaystyle \widetilde S_i=\left\{\begin{array}{ll} S_i^{(1)}\,, & \mbox{fall...
... i>N^{(1)}_{\mathbb{R}^d}$,}\\ [3\jot] \infty &\mbox{sonst} \end{array}\right.$](img2287.png) |
(12) |
eine messbare Indizierung der Atome des zufälligen Maßes 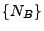 mit
mit
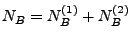 gegeben ist.
gegeben ist.
Wir übertragen nun den in (12) gegebenen Ansatz auf
den Fall von beliebigen (endlichen bzw. abzählbar unendlichen)
Summen unabhängiger Poisson-Prozesse.
Theorem 4.11
Sei
![$ \mu:\mathcal{B}(\mathbb{R}^d)\to[0,\infty]$](img2193.png)
ein beliebiges diffuses und
lokal endliches Maß. Dann gibt es eine Folge
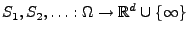
von Zufallsvektoren,
so dass das zufällige Zählmaß
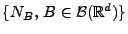
mit
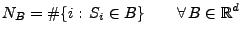 |
(13) |
ein Poisson-Prozess mit dem Intensitätsmaß
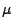
ist.
- Beweis
-




Nächste Seite: Simulationsalgorithmus; Akzeptanz- und Verwerfungsmethode
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Definition und elementare Eigenschaften
Inhalt
Ursa Pantle
2005-07-13
![]() und
somit die mathematische Grundlage von Simulationsalgorithmen
bildet, vgl. auch die Abschnitte 4.2.3 und
4.2.4.
und
somit die mathematische Grundlage von Simulationsalgorithmen
bildet, vgl. auch die Abschnitte 4.2.3 und
4.2.4.
![]() diffus ist, d.h., es gelte
diffus ist, d.h., es gelte