



Nächste Seite: Prozesse mit stückweise konstanten
Aufwärts: Einleitung
Vorherige Seite: Modifikationen von càdlàg Prozessen
Inhalt
Stationarität und Unabhängigkeit; stationäre bzw.
unabhängige Zuwächse
Von großer Bedeutung sind stochastische Prozesse, für die die in
(1.2.1) eingeführten endlich-dimensionalen
Verteilungen gewisse Invarianzeigenschaften besitzen. Zwei
wichtige Klassen solcher stochastischen Prozesse sind wie folgt
definiert.
- Definition
 Seien
Seien
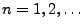 ,
,
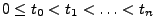 und
und 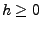 beliebige Zahlen.
beliebige Zahlen.
- Der stochastische Prozess
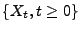 heißt stationär,
wenn
die Verteilungen der Zufallsvektoren
heißt stationär,
wenn
die Verteilungen der Zufallsvektoren
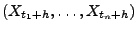 nicht von
nicht von 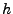 abhängen.
abhängen.
- Man sagt, dass der stochastische Prozess
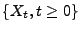 ein
Prozess mit stationären Zuwächsen ist, wenn die
Verteilungen der Zufallsvektoren
ein
Prozess mit stationären Zuwächsen ist, wenn die
Verteilungen der Zufallsvektoren
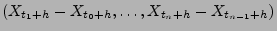 nicht von
nicht von 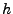 abhängen.
abhängen.
Eine andere wichtige Klasse von stochastischen Prozessen, die wir
in dieser Vorlesung ausführlich behandeln werden, ist wie folgt
definiert.
- Definition
 Man
sagt, dass der stochastische Prozess
Man
sagt, dass der stochastische Prozess
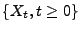 ein Prozess mit unabhängigen Zuwächsen ist, wenn die
Zufallsvariablen
ein Prozess mit unabhängigen Zuwächsen ist, wenn die
Zufallsvariablen 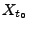 ,
,
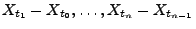 für alle
für alle
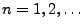 und
und
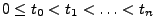 unabhängig sind.
unabhängig sind.
Gelegentlich werden wir auch den Begriff der Unabhängigkeit von
zwei (oder mehreren) stochastischen Prozessen bzw. den Begriff der
Unabhängigkeit eines Prozesses von einer  -Algebra
benötigen.
-Algebra
benötigen.
- Definition
 Seien
Seien
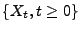 und
und
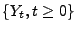 zwei beliebige stochastische Prozesse über einunddemselben
Wahrscheinlichkeitsraum
zwei beliebige stochastische Prozesse über einunddemselben
Wahrscheinlichkeitsraum
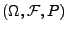 und sei
und sei
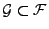 eine beliebige Teil-
eine beliebige Teil- -Algebra von
-Algebra von
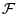 .
.
- Man sagt dann, dass
 und
und 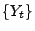 unabhängig sind,
wenn die Zufallsvektoren
unabhängig sind,
wenn die Zufallsvektoren
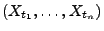 und
und
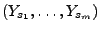 für beliebige (endliche) Folgen von
nichtnegativen Zahlen
für beliebige (endliche) Folgen von
nichtnegativen Zahlen
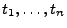 bzw.
bzw.
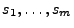 unabhängig sind.
unabhängig sind.
- Außerdem sagt man, dass
 von
von
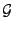 unabhängig
ist, wenn für jede Folge
unabhängig
ist, wenn für jede Folge
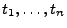 von nichtnegativen
Zahlen und für beliebige
von nichtnegativen
Zahlen und für beliebige
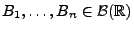 und
und
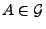 die Ereignisse
die Ereignisse
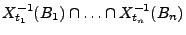 und
und 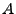 unabhängig sind, wobei
unabhängig sind, wobei
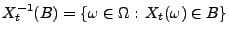 .
.




Nächste Seite: Prozesse mit stückweise konstanten
Aufwärts: Einleitung
Vorherige Seite: Modifikationen von càdlàg Prozessen
Inhalt
Ursa Pantle
2005-07-13
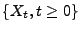 heißt stationär,
wenn
die Verteilungen der Zufallsvektoren
heißt stationär,
wenn
die Verteilungen der Zufallsvektoren
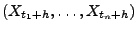 nicht von
nicht von 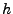 abhängen.
abhängen.
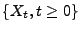 ein
Prozess mit stationären Zuwächsen ist, wenn die
Verteilungen der Zufallsvektoren
ein
Prozess mit stationären Zuwächsen ist, wenn die
Verteilungen der Zufallsvektoren
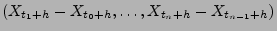 nicht von
nicht von 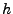 abhängen.
abhängen.