



Nächste Seite: Regularität der Trajektorien
Aufwärts: Einleitung
Vorherige Seite: Grundbegriffe
Inhalt
Endlich-dimensionale Verteilungen; Existenzsatz von Kolmogorow
Sei
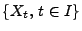 ein stochastischer Prozess mit
ein stochastischer Prozess mit
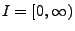 und
und
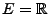 .
.
- Definition
 Für jedes
Für jedes
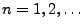 und für jedes
und für jedes 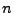 -Tupel
-Tupel
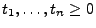 von Indizes wird die
Mengenfunktion
von Indizes wird die
Mengenfunktion
![$ P_{t_1,\ldots,t_n}:\mathcal{B}(\mathbb{R}^n)\to[0,1]$](img34.png) mit
mit
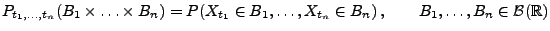 |
(1) |
endlich-dimensionale Verteilung von  genannt.
genannt.
- Beachte
 Es ist klar, dass die endlich-dimensionalen Verteilungen von
stochastischen Prozessen die folgenden Konsistenzeigenschaften besitzen.
Es ist klar, dass die endlich-dimensionalen Verteilungen von
stochastischen Prozessen die folgenden Konsistenzeigenschaften besitzen.
Wir nehmen nun umgekehrt an, dass
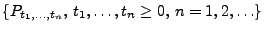 eine
beliebige Familie von Wahrscheinlichkeitsmaßen ist, die den
Bedingungen (2) und (3) genügen.
eine
beliebige Familie von Wahrscheinlichkeitsmaßen ist, die den
Bedingungen (2) und (3) genügen.
Der folgende (Existenz-) Satz von Kolmogorow ist eine wichtige
Fundamentalaussage in der Theorie stochastischer Prozesse.
Theorem 1.1

Für jede Familie von Wahrscheinlichkeitsmaßen
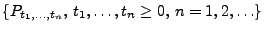
, die
den Bedingungen
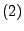
und
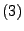
genügen, gibt es einen Wahrscheinlichkeitsraum
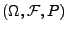
und einen stochastischen Prozess

über diesem
Wahrscheinlichkeitsraum, so dass
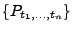
die
endlich-dimensionalen Verteilungen von

sind.
Der Beweis von Theorem 1.1 beruht auf
Standard-Techniken der Maßtheorie. Wir erwähnen hier nur die
Grundidee des Kolmogorowschen Konstruktionsprinzips. Ein
detaillierter Beweis kann zum Beispiel in Kallenberg (2001), S.
115-116 nachgelesen werden.
Dabei wird bei der Wahl eines geeigneten Wahrscheinlichkeitsraumes
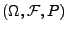 bzw. des zugehörigen stochastischen Prozesses
bzw. des zugehörigen stochastischen Prozesses
 wie folgt vorgegangen.
wie folgt vorgegangen.
- Beachte

- Der Existenzsatz von Kolmogorow gilt auch für
beliebige Indexmengen
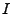 und für beliebige Zustandsräume
und für beliebige Zustandsräume
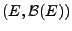 , d.h.,
für Familien von Wahrscheinlichkeitsmaßen
, d.h.,
für Familien von Wahrscheinlichkeitsmaßen
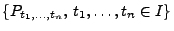 über
über
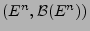 mit
mit
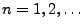 , die den Bedingungen
, die den Bedingungen
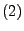 und
und
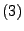 genügen.
genügen.
- Der stochastische Koordinaten-Prozess
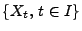 wird
dann auf völlig analoge Weise über dem Wahrscheinlichkeitsraum
wird
dann auf völlig analoge Weise über dem Wahrscheinlichkeitsraum
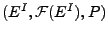 konstruiert, wobei
konstruiert, wobei
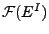 die kleinste
die kleinste
 -Algebra ist, die alle Zylinger-Mengen von
-Algebra ist, die alle Zylinger-Mengen von 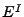 enthält.
enthält.




Nächste Seite: Regularität der Trajektorien
Aufwärts: Einleitung
Vorherige Seite: Grundbegriffe
Inhalt
Ursa Pantle
2005-07-13
![]() ein stochastischer Prozess mit
ein stochastischer Prozess mit
![]() und
und
![]() .
.
![]() bzw. des zugehörigen stochastischen Prozesses
bzw. des zugehörigen stochastischen Prozesses
![]() wie folgt vorgegangen.
wie folgt vorgegangen.