Modifikationen von càdlàg Prozessen

In diesem und in den nachfolgenden Abschnitten setzen wir stets (o.B.d.A.) voraus, dass 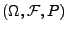$(\Omega,\mathcal{F},P)$ ein vollständiger Wahrscheinlichkeitsraum ist, d.h.,

• sämtliche ,,Nullmengen'' des Wahrscheinlichkeitsraumes 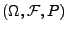$(\Omega,\mathcal{F},P)$ gehören zu 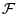$\mathcal{F}$ bzw. (äquivalent hierzu)
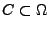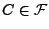• für $C\subset\Omega$ gilt $C\in\mathcal{F}$, falls es Teilmengen 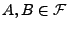$A,B\in\mathcal{F}$ gibt, so dass 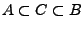$A\subset C\subset B$ und $P(B\setminus A)=0$.

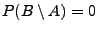Beachte

 

• Zur Erinnerung: Wenn für die stochastischen Prozesse $\{X_t,\,t\ge 0\}$ und $\{Y_t,\,t\ge 0\}$

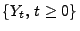
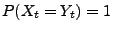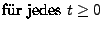  $$P(X_t=Y_t)=1 \mbox{für jedes $t\ge 0$}$$ (5)

  
  
  gilt, dann wird 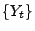$\{Y_t\}$ eine Modifikation von $\{X_t\}$ (und umgekehrt) genannt.
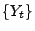• Manchmal wird eine verschärfte Version der Bedingung (5) betrachtet. Dabei sagt man, dass die stochastischen Prozesse $\{X_t\}$ und $\{Y_t\}$ ununterscheidbar sind, wenn
  $$P(X_t=Y_t\;$$$$\mbox{für jedes $t\ge 0$}$$$$\,)=1\,.$$

• Außerdem sagt man, dass der stochastische Prozess $\{X_t,\,t\ge 0\}$ càdlàg ist,
  • wenn fast alle Trajektorien von $\{X_t\}$ rechtsstetige Funktionen sind, die linksseitige Grenzwerte besitzen,
  • wobei ,,càdlàg'' eine Abkürzung der französischen Sprechweise ,,continu à droite, limites à gauche'' ist.
• Alle stochastischen Prozesse mit stückweise konstanten bzw. stetigen Trajektorien, die in Kapitel 2 betrachtet wurden, sind càdlàg.

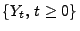
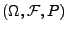
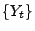
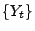
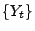
Theorem 1.4   $\;$ Seien $\{X_t,\,t\ge 0\}$ und $\{Y_t,\,t\ge 0\}$ stochastische Prozesse über $(\Omega,\mathcal{F},P)$, so dass $\{X_t\}$ und $\{Y_t\}$ mit Wahrscheinlichkeit $1$ rechtsstetige Trajektorien besitzen. Außerdem sei $\{Y_t\}$ eine Modifikation von $\{X_t\}$. Dann sind die Prozesse $\{X_t\}$ und $\{Y_t\}$ ununterscheidbar.

Beweis

 

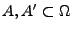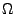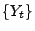• Seien $A,A^\prime\subset\Omega$ diejenigen Teilmengen von $\Omega$, für die die Trajektorien von $\{X_t\}$ bzw. $\{Y_t\}$ nicht rechtsstetig sind, wobei dann $P(A)=P(A^\prime)=0$.
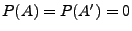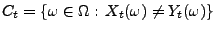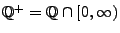• Außerdem sei $C_t=\{\omega\in\Omega:\,X_t(\omega)\not= Y_t(\omega)\}$ für jedes $t\ge 0$ und $C=\bigcup_{t\in\mathbb{Q}^+} C_t$, wobei $\mathbb{Q}^+=\mathbb{Q}\cap[0,\infty)$ die Menge der rationalen Zahlen in 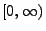$[0,\infty)$ bezeichnet.
  • Weil $\{Y_t\}$ eine Modifikation von $\{X_t\}$ ist, gilt $P(C)=0$ und deshalb auch

    $$P(C^\prime)=0\,,$$ (6)

    
    
    wobei $C^\prime=C\cup A\cup A^\prime$.
  • Somit ist klar, dass $X_t(\omega)= Y_t(\omega)$ für beliebige $t\in\mathbb{Q}^+$ und $\omega\not\in C^\prime$.
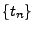• Sei nun $t\ge 0$ eine beliebige (nichtnegative) Zahl und $\{t_n\}$ eine Folge rationaler Zahlen mit 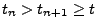$t_n>t_{n+1}\ge t$ und $t_n\downarrow t$.
  • Weil $X_{t_n}(\omega)= Y_{t_n}(\omega)$ für beliebige $n\ge 1$ und $\omega\not\in C^\prime$, ergibt sich nun, dass
    $$X_t(\omega)= \lim_{n\to\infty} X_{t_n}(\omega)= \lim_{n\to\infty} Y_{t_n}(\omega)=Y_t(\omega)$$
    für beliebige $t\ge 0$ und $\omega\not\in C^\prime$.
  • Wegen (6) folgt hieraus, dass die Prozesse $\{X_t\}$ und $\{Y_t\}$ ununterscheidbar sind.
    
    $\Box$

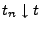Aus Theorem 1.4 ergibt sich insbesondere das folgende Resultat.

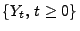
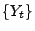
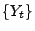
Korollar 1.1   Die Prozesse $\{X_t,\,t\ge 0\}$ und $\{Y_t,\,t\ge 0\}$ seien càdlàg, wobei $\{Y_t\}$ eine Modifikation von $\{X_t\}$ sei. Dann sind die Prozesse $\{X_t\}$ und $\{Y_t\}$ ununterscheidbar.