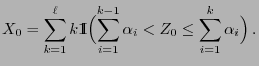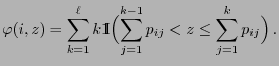Next: Determining the Rate of
Up: Reversibility; Estimates for the
Previous: Definition and Examples
Contents
Recursive Construction of the ,,Past''
- Recall that
- If the pair
 is reversible, then the stationary
Markov chain
is reversible, then the stationary
Markov chain
 constructed in
(92)-(94) can be tracked back
into the past in the following way.
constructed in
(92)-(94) can be tracked back
into the past in the following way.
Theorem 2.14
- Let
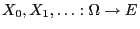 be a reversible Markov chain with
state space
be a reversible Markov chain with
state space 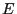 , transition matrix
, transition matrix
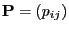 and stationary
initial distribution
and stationary
initial distribution
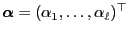 .
.
- Then the sequence
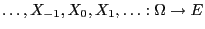 defined
by
defined
by
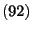 -
-
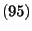 is
is
The proof of Theorem 2.14 is quite similar
to the ones given for Theorems 2.11 and 2.13
and is therefore omitted.




Next: Determining the Rate of
Up: Reversibility; Estimates for the
Previous: Definition and Examples
Contents
Ursa Pantle
2006-07-20
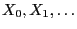 with transition matrix
with transition matrix
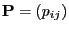 and stationary initial
distribution
and stationary initial
distribution
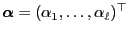 can be
constructed as follows, where
can be
constructed as follows, where
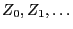 of independent and on
of independent and on
![$ [0,1]$](img137.png) uniformly distributed random variables and defined
for all
uniformly distributed random variables and defined
for all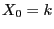 if and only if
if and only if![$\displaystyle \qquad
Z_0\in\Bigl(\sum_{i=1}^{k-1}
\alpha_i,\sum_{i=1}^{k}\alpha_i\Bigr]\,,
$](img168.png)
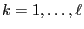 , i.e.
, i.e.
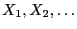 were defined by the recursion
formula
were defined by the recursion
formula
![$ \varphi:E\times[0,1]\to E$](img753.png) was given by
was given by
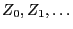 of
independent and on
of
independent and on ![$ [0,1]$](img137.png) uniformly distributed random variables
to a sequence
uniformly distributed random variables
to a sequence
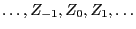 of independent and
identically random variables that is unbounded in both directions.
of independent and
identically random variables that is unbounded in both directions.
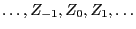 this expansion does not pose any
problems as the underlying probability space can be constructed
via an appropriate product space, product-
this expansion does not pose any
problems as the underlying probability space can be constructed
via an appropriate product space, product- -algebra, and
product measure.
-algebra, and
product measure.
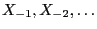 are now constructed
recursively setting
are now constructed
recursively setting
![$ \varphi:E\times[0,1]\to E$](img753.png) is defined in
(94).
is defined in
(94).