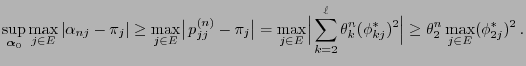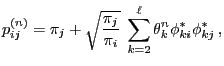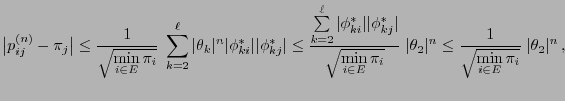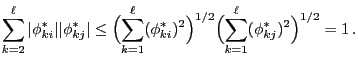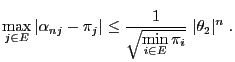Next: Multiplicative Reversible Version of
Up: Reversibility; Estimates for the
Previous: Recursive Construction of the
Contents
Determining the Rate of Convergence under Reversibility
- Remarks
-
- Notice that (97) yields the following more precise
specification of the convergence estimate (96).
We have
as the column vectors
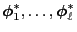 and
hence also the row vectors
and
hence also the row vectors
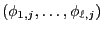 where
where
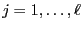 form an orthonormal basis in
form an orthonormal basis in
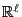 and thus by the Chauchy-Schwarz inequality
and thus by the Chauchy-Schwarz inequality
- Consequently,
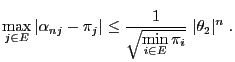 |
(98) |
- However, the practical benefit of the estimate (98)
can be limited for several reasons:
- The factor in front of
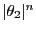 in (98) does
not depend on the choice of the initial distribution
in (98) does
not depend on the choice of the initial distribution
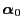 .
.
- The derivation of the estimate (98) requires the
Markov chain to be reversible.
- It can be difficult to determine the eigenvalue
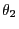 if the
number of states is large.
if the
number of states is large.
- Therefore in Section 2.3.5 we consider an alternative convergence estimate,
- which depends on the initial distribution
- and does not require the reversibility of the Markov chain.
- Furthermore, in Section 2.3.7 we will derive an upper
bound for the second largest absolute value
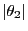 among the
eigenvalues of a reversible transition matrix.
among the
eigenvalues of a reversible transition matrix.




Next: Multiplicative Reversible Version of
Up: Reversibility; Estimates for the
Previous: Recursive Construction of the
Contents
Ursa Pantle
2006-07-20
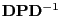 where
where
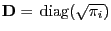 .
.
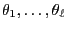 of
of
 coincide
with the eigenvalues of
coincide
with the eigenvalues of
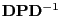 we obtain
we obtain
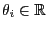 for all
for all 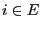 ,
,
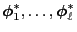 of
of
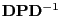 can be chosen such that all of their
components are real,
can be chosen such that all of their
components are real,
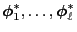 are also left
eigenvectors of
are also left
eigenvectors of
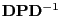 and that the rows as well
as the lines of the
and that the rows as well
as the lines of the
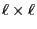 matrix
matrix
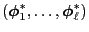 are orthonormal vectors.
are orthonormal vectors.
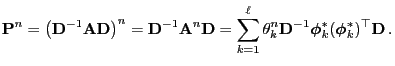
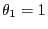 and
and
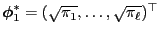 we obtain
for arbitrary
we obtain
for arbitrary 
 is even or all eigenvalues
is even or all eigenvalues
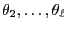 are nonnegative, then
are nonnegative, then