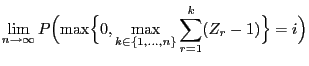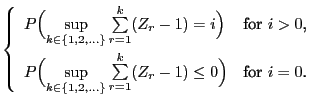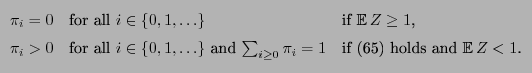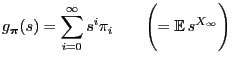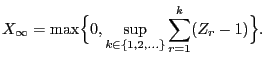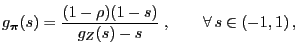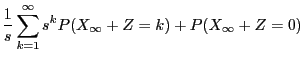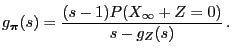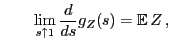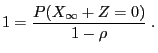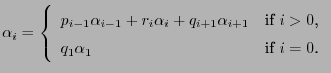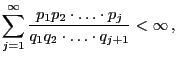Next: Direct and Iterative Computation
Up: Ergodicity and Stationarity
Previous: Irreducible and Aperiodic Markov
Contents
Stationary Initial Distributions
- Recall
- If the Markov chain
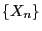 is not assumed to be irreducible there
can be more than one solution for (59).
is not assumed to be irreducible there
can be more than one solution for (59).
- Conversely, it is possible to show that
- there is a unique probability solution
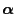 for the
matrix equation (59) if
for the
matrix equation (59) if
 is irreducible.
is irreducible.
- However, this solution
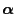 of (59) is not
necessarily the limit distribution
of (59) is not
necessarily the limit distribution
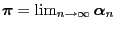 as
as
 does not exist
if
does not exist
if
 is not aperiodic.
is not aperiodic.
A proof of Theorem 2.10 can be found in
Chapter 7 of E. Behrends (2000) Introduction to Markov
Chains, Vieweg, Braunschweig.
- Remarks
-
- Besides the invariance property
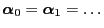 ,
the Markov chain
,
the Markov chain 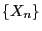 with stationary initial distribution
with stationary initial distribution
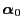 exhibits still another invariance property for all finite dimensional distributions that is considerably
stronger.
exhibits still another invariance property for all finite dimensional distributions that is considerably
stronger.
- In this context we consider the following notion of a (strongly)
stationary sequence of random variables.
- Definition
-
Theorem 2.11
- Let
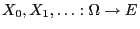 be a Markov chain with state space
be a Markov chain with state space
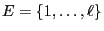 .
.
- Then
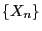 is a stationary sequence of random variables if and
only if the Markov chain
is a stationary sequence of random variables if and
only if the Markov chain 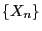 has a stationary initial
distribution.
has a stationary initial
distribution.
- Proof
-
- The necessity of the condition follows immediately
- from Theorem 2.3 and from the
definitions for a stationary initial distribution and a stationary
sequence of random variables, respectively,
- as (62) in particular implies that
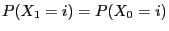 for all
for all 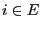
- and from Theorem 2.3 we thus obtain
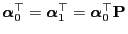 , i.e.,
, i.e.,
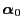 is a stationary initial distribution.
is a stationary initial distribution.
- Conversely, suppose now that
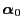 is a stationary initial
distribution of the Markov chain
is a stationary initial
distribution of the Markov chain 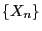 .
.
- Remarks
-
- For some Markov chains, whose transition matrices exhibit a
specific structure, we already calculated their stationary initial
distributions in Sections 2.2.2 and
2.2.3.
- Now we will discuss two additional examples of this type.
- In these examples the state space is infinite requiring an
additional condition apart from quasi-positivity (or
irreducibility and aperiodicity) in order to ensure the ergodicity
of the Markov chains.
- Namely, a so-called contraction condition is imposed that
prevents the probability mass to ,,migrate towards infinity''.
- Examples
-
- Queues
see. T. Rolski, H. Schmidli, V. Schmidt, J. Teugels (2002)
Stochastic Processes for Insurance and Finance.
J. Wiley & Sons, Chichester, S. 147 ff.
- We consider the example already discussed in
Section 2.1.2
- of the recursively defined Markov chain
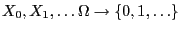 with
with 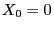 and
and
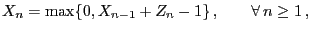 |
(63) |
- where the random variables
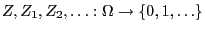 are independent and
identically distributed and the transition matrix
are independent and
identically distributed and the transition matrix
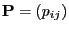 is given by
is given by
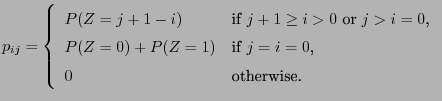 |
(64) |
- It is not difficult to show that
- the Markov chain
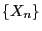 defined by the recursion formula
(63) with its corresponding transition matrix
(64) is irreducible and aperiodic if
defined by the recursion formula
(63) with its corresponding transition matrix
(64) is irreducible and aperiodic if
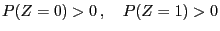 and and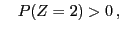 |
(65) |
- for all
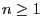 the solution of the recursion equation
(63) can be written as
the solution of the recursion equation
(63) can be written as
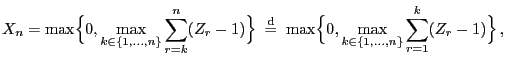 |
(66) |
- the limit probabilities
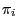 exist for all
exist for all
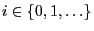 where
where
- Furthermore
- Thus, for Markov chains with (countably) infinite state space,
- irreducibility and aperiodicity do not always imply
ergodicity,
- but, additionally, a certain contraction condition needs to
be satisfied,
- where in the present example this condition is the requirement of
a negative drift , i.e.,
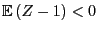 .
.
- If the conditions (65) are satisfied and
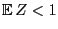 , then
, then
- Proof of (68)
- By the defibition (67) of
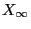 , we have
, we have
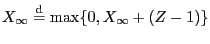 .
.
- Furthermore, using the notation
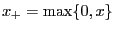 , we obtain
, we obtain
i.e.
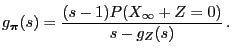 |
(69) |
- As
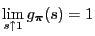
and
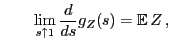
by L'Hospital's rule we can conclude that
- Hence (68) is a consequence of (69).
- Birth and death processes with one reflecting barrier




Next: Direct and Iterative Computation
Up: Ergodicity and Stationarity
Previous: Irreducible and Aperiodic Markov
Contents
Ursa Pantle
2006-07-20
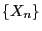 is an irreducible and aperiodic Markov chain with
(finite) state space
is an irreducible and aperiodic Markov chain with
(finite) state space
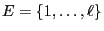 and (quasi-positive)
transition matrix
and (quasi-positive)
transition matrix
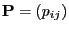 ,
,
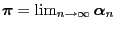 is the uniquely determined probability solution of the following
matrix equation (see Theorem 2.5):
is the uniquely determined probability solution of the following
matrix equation (see Theorem 2.5):