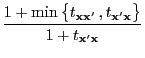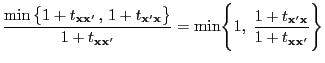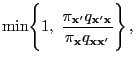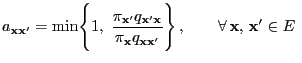- The transition matrix
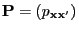 can be of a
more general form than the one defined by
can be of a
more general form than the one defined by
- Besides this, a procedure for acceptance or rejection of the
updates
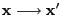 is integrated into the
algorithm. It is based on a similar idea as the
acceptance-rejection sampling discussed in
Section 3.2.3; see in particular
Theorem 3.5.
is integrated into the
algorithm. It is based on a similar idea as the
acceptance-rejection sampling discussed in
Section 3.2.3; see in particular
Theorem 3.5.
- taking values in the finite state space
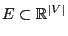 with
probability
with
probability 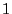 .
.
- As usual we assume
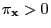 for all
for all
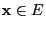 where
where
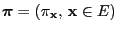 is the probability function of the
random vector
is the probability function of the
random vector
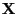 .
.
- where
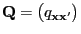 is an arbitrary
stochastic matrix that is irreducible and aperiodic, i.e. in
particular
is an arbitrary
stochastic matrix that is irreducible and aperiodic, i.e. in
particular
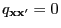 if and only if
if and only if
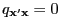 .
.
- Moreover, the matrix
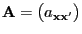 is
defined as
is
defined as
where
- and
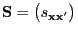 is an arbitrary
symmetric matrix such that
is an arbitrary
symmetric matrix such that
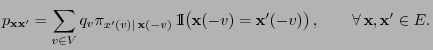
![$\displaystyle t_{{\mathbf{x}}{\mathbf{x}}^\prime}=\left\{\begin{array}{ll}\disp...
...3\jot] 0 &\mbox{if $q_{{\mathbf{x}}{\mathbf{x}}^\prime}=0$,} \end{array}\right.$](img1656.png)