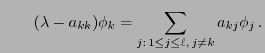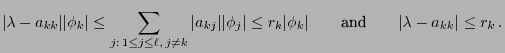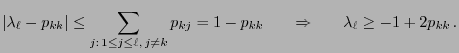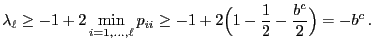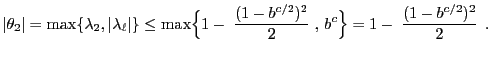- in order to determine upper bounds for the distance
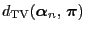 occurring in the
occurring in the  th step of the MCMC
simulation via the Metropolis algorithm,
th step of the MCMC
simulation via the Metropolis algorithm,
- if the simulated distribution
 satisfies the following
conditions.
satisfies the following
conditions.
- that
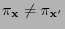 for arbitrary
for arbitrary
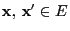 such that
such that
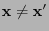 ,
,
- and that the states
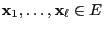 are ordered
such that
are ordered
such that
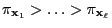 .
.
- where
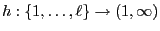 is a monotonically
increasing function,
is a monotonically
increasing function,
- and
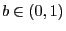 is chosen such that for a certain constant
is chosen such that for a certain constant 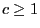
- and
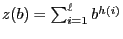 is an (in general unknown)
factor.
is an (in general unknown)
factor.
- that the basis
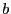 and the differences
and the differences
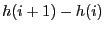 are known for
all
are known for
all
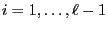 ,
,
- i.e. in particular that the quotients
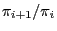 are known
for all
are known
for all
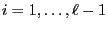 .
.
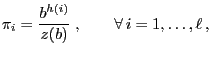
![$\displaystyle q_{ij}=\left\{\begin{array}{ll} \displaystyle\frac{1}{2} &\mbox{i...
...,\ell-1$\ and $j=i-1,\,i+1$,}\\ [3\jot] 0\,, & \mbox{else.} \end{array}\right.$](img1710.png)
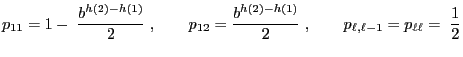
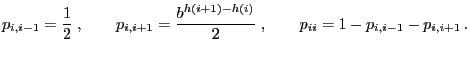
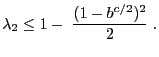
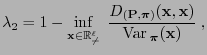
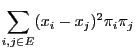
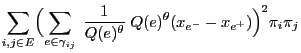
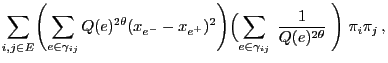
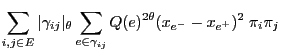
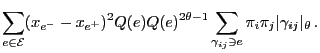
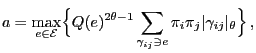
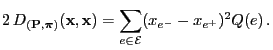
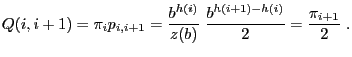
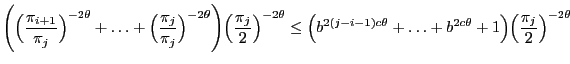
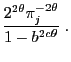
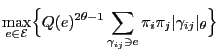
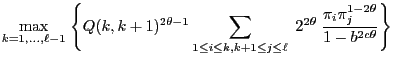
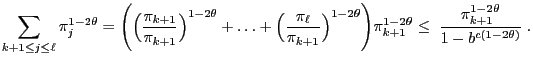
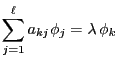 and
and