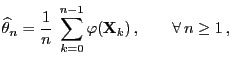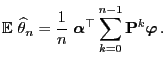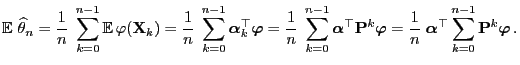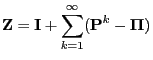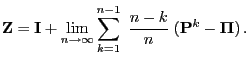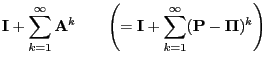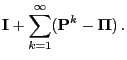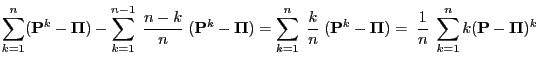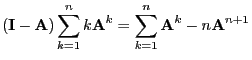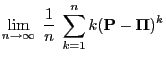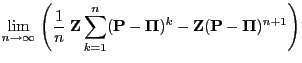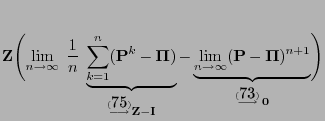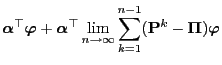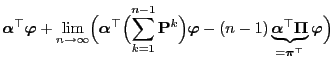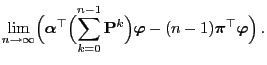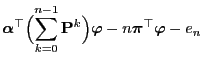Next: Asymptotic Variance of Estimation;
Up: Error Analysis for MCMC
Previous: Estimate for the Rate
Contents
MCMC Estimators; Bias and Fundamental Matrix
In this section we will investigate the characteristics of
Monte-Carlo estimators for expectations.
- Examples for similar problems were already discussed in
Section 3.1.1,
- when we estimated
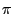 by statistical means
by statistical means
- and the value of integrals via Monte-Carlo simulation.
- However, for these purposes we assumed
- that the pseudo-random numbers can be regarded as realizations of
independent and identically distributed sampling variables.
- In the present section we assume that the sample variables form an
(appropriately chosen) Markov chain.
- This is the reason why these estimators are called Markov-Chain-Monte-Carlo estimators (MCMC estimators).
- Statistical Model
-
- Remarks
-
- Typically, the initial distribution
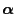 does not
coincide with the simulated distribution
does not
coincide with the simulated distribution
 .
.
- Consequently, the MCMC estimator
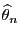 defined by
(70) is not unbiased for fixed (finite) sample size,
defined by
(70) is not unbiased for fixed (finite) sample size,
- i.e. in general
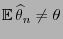 for all
for all 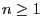 .
.
- For determining the bias
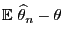 the
following representation formula will be helpful.
the
following representation formula will be helpful.
- Proof
-
- Remarks
-
- As an immediate consequence of Theorem 3.17, the
ergodicity of the transition matrix
 , and
(69), one obtains
, and
(69), one obtains
- i.e., the MCMC estimator
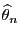 for
for 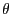 defined
in (70) is asymptotically unbiased.
defined
in (70) is asymptotically unbiased.
Apart from this, the asymptotic behavior of
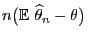 for
for
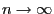 can be
determined. For this purpose we need the following two lemmata.
can be
determined. For this purpose we need the following two lemmata.
Lemma 3.2

Let
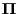
be the
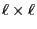
matrix consisting of the
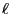
identical row vectors
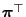
. Then
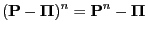 |
(72) |
for all
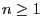
and in particular
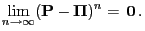 |
(73) |
- Proof
-
- Remarks
-
Lemma 3.3

The fundamental matrix
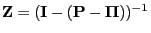
of the
irreducible and aperiodic transition matrix

has the
representation formulae
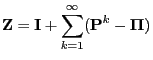 |
(75) |
and
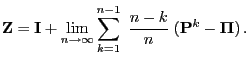 |
(76) |
- Proof
-
- Formula (75) follows from Lemmas 2.4 and
3.2 as for
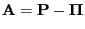
- In order to show (76) it suffices to notice that
and that the last expression converges to
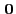 for
for
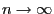 .
.
- The zero convergence is due to the fact that for every
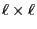 matrix
matrix
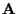 and thus for
and thus for
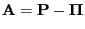

Theorem 3.17 and Lemma 3.3 enable us to
give a more detailed description of the asymptotic behavior of the
bias
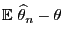 .
.
- Proof
-
- The representation formula (75) in
Lemma 3.3 yields
- Hence by taking into account Theorem 3.17 we obtain
the following for a certain sequence
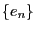 such that
such that 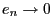 :
:





Next: Asymptotic Variance of Estimation;
Up: Error Analysis for MCMC
Previous: Estimate for the Rate
Contents
Ursa Pantle
2006-07-20
 by statistical means
by statistical means