bzw.
- Konfidenzintervall für die Linearkombination
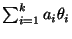 der Erwartungswerte
der Erwartungswerte
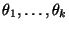 bzw. einen
bzw. einen
- Test zur Verifizierung der Hypothese
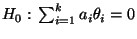
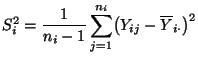
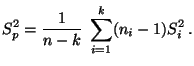
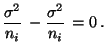 |
Durch eine geeignete Wahl des Vektors
![]() ergeben sich aus
(61) Tests spezifischer Eigenschaften der
Erwartungswerte
ergeben sich aus
(61) Tests spezifischer Eigenschaften der
Erwartungswerte
![]() .
.