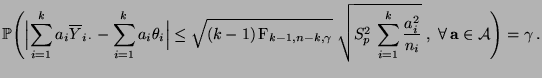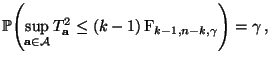Next: Multiples lineares Regressionsmodell
Up: Einfaktorielle Varianzanalyse
Previous: F-Test der ANOVA-Nullhypothese; Quadratsummenzerlegung
Contents
Simultane Konfidenzbereiche für Kontraste
In Verallgemeinerung des in (62) hergeleiteten
Konfidenzintervalls für einen einzelnen Kontrast lassen sich (auf
ähnliche Weise wie in Abschnitt 2.1.6) mit Hilfe der
Bonferroni-Ungleichung (46) simultane
Konfidenzbereiche zum Niveau
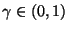 gleichzeitig für
meherere Kontraste angeben.
gleichzeitig für
meherere Kontraste angeben.
- Beispiele
-
- Zunächst betrachten wir die Differenzen
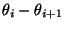 der Erwartungswerte benachbarter Teilstichproben, d.h., wir
bestimmen einen simultanen Konfidenzbereich für die Kontraste
der Erwartungswerte benachbarter Teilstichproben, d.h., wir
bestimmen einen simultanen Konfidenzbereich für die Kontraste
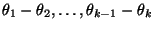 zum Niveau
zum Niveau
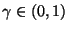 .
.
- Sei
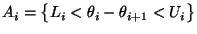 für jedes
für jedes
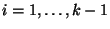 , wobei
und
, wobei
und
- Dann ergibt sich aus der Bonferroni-Ungleichung
(46) und aus (62), daß
- Auf ähnliche Weise ergibt sich ein simultaner Konfidenzbereich für
die Differenzen
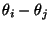 der Erwartungswerte sämtlicher
Paare von Teilstichproben, d.h., wir bestimmen nun einen
simultanen Konfidenzbereich für die Kontraste
der Erwartungswerte sämtlicher
Paare von Teilstichproben, d.h., wir bestimmen nun einen
simultanen Konfidenzbereich für die Kontraste
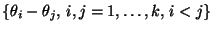 zum Niveau
zum Niveau
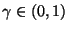 .
.
- Und zwar sei
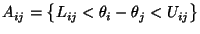 für beliebige
für beliebige
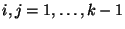 mit
mit 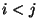 , wobei
und
, wobei
und
- Dann ergibt sich aus der Bonferroni-Ungleichung
(46) und aus (62), daß
Auf ähnliche Weise, wie in Theorem 2.9 ein
Konfidenzband für die Regressionsgerade
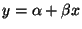 hergeleitet wurde, läßt sich ein simultaner Konfidenzbereich zum
Niveau
hergeleitet wurde, läßt sich ein simultaner Konfidenzbereich zum
Niveau 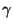 für sämtliche Kontraste
für sämtliche Kontraste
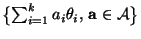 konstruieren.
konstruieren.
Theorem 2.14

Mit Wahrscheinlichkeit
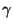
gilt
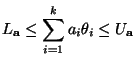 |
(75) |
gleichzeitig für jedes
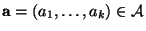
, wobei
und
- Beweis
-
- Die Behauptung ist äquivalent mit
bzw. mit
wobei
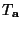 in (65) gegeben ist.
in (65) gegeben ist.
- Die Gültigkeit der letzten Gleichheit wurde bereits in
Theorem 2.12 bewiesen.

- Beachte
 Man kann zeigen, daß (75) mit
Wahrscheinlichkeit
Man kann zeigen, daß (75) mit
Wahrscheinlichkeit 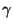 sogar gleichzeitig für jeden beliebigen Vektor
sogar gleichzeitig für jeden beliebigen Vektor
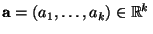 gilt, falls
die Definitionsgleichungen für die Schranken
gilt, falls
die Definitionsgleichungen für die Schranken
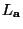 und
und
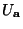 geringfügig geändert werden, vgl. Übungsaufgabe 6.2.
geringfügig geändert werden, vgl. Übungsaufgabe 6.2.




Next: Multiples lineares Regressionsmodell
Up: Einfaktorielle Varianzanalyse
Previous: F-Test der ANOVA-Nullhypothese; Quadratsummenzerlegung
Contents
Ursa Pantle
2003-03-10
![]() gleichzeitig für
meherere Kontraste angeben.
gleichzeitig für
meherere Kontraste angeben.
![]() hergeleitet wurde, läßt sich ein simultaner Konfidenzbereich zum
Niveau
hergeleitet wurde, läßt sich ein simultaner Konfidenzbereich zum
Niveau ![]() für sämtliche Kontraste
für sämtliche Kontraste
![]() konstruieren.
konstruieren.