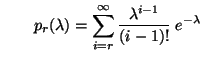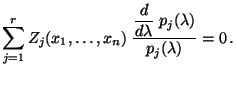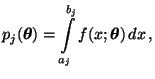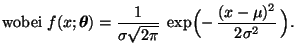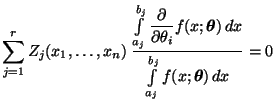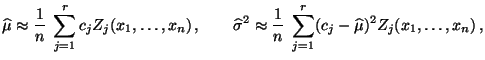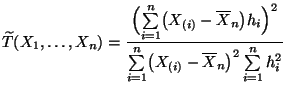- Mit Hilfe von Theorem 5.3 soll durch die Beobachtung
der (unabhängigen und identisch verteilten) Zufallsvariablen
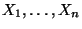 zunächst geprüft werden, ob die Verteilung
zunächst geprüft werden, ob die Verteilung 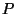 von
von 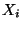 zur Familie der Poisson-Verteilungen gehört.
zur Familie der Poisson-Verteilungen gehört.
- Sei also
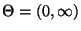 mit
mit
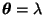 , und sei
, und sei
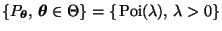 die Familie der Poisson-Verteilungen.
die Familie der Poisson-Verteilungen.
- Wir betrachten die folgenden
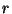 Klassen
Klassen
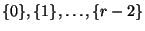 und
und
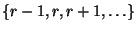 , d.h.
, d.h.
![$\displaystyle (a_1,b_1]=(-\infty,0],\quad(a_2,b_2]=(0,1],\quad\ldots
\quad(a_{r-1},b_{r-1}=(r-3,r-2],\quad(a_r,b_r]=(r-2,\infty)\,.
$](img2409.png)
- Die Wahrscheinlichkeiten
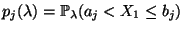 sind dann gegeben durch
sind dann gegeben durch
- Gemäß (33) genügt jeder
Maximum-Likelihood-Schätzer
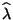 für
für 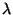 , der
aus den gruppierten Daten gewonnen wird, der Gleichung
, der
aus den gruppierten Daten gewonnen wird, der Gleichung
- Dabei ergibt sich aus (47), daß
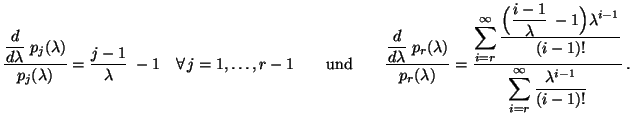
- Hieraus und aus (48) folgt, daß der ML-Schätzer
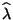 der folgenden Gleichung genügt:
der folgenden Gleichung genügt:
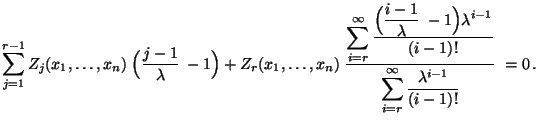
- Für jedes
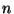 gibt es ein
gibt es ein
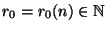 , so daß
, so daß
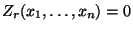 für jedes
für jedes 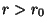 . Hieraus folgt, daß für
. Hieraus folgt, daß für
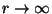
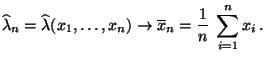
- Bei einer hinreichend großen Anzahl
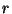 von Klassen
von Klassen
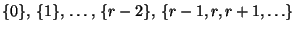 bildet
also das Stichprobenmittel
bildet
also das Stichprobenmittel
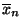 , das eine ML-Schätzung
für
, das eine ML-Schätzung
für 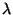 im ungruppierten Poisson-Modell ist, eine gute
Näherung für die ML-Schätzung
im ungruppierten Poisson-Modell ist, eine gute
Näherung für die ML-Schätzung
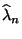 für
für 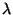 im
gruppierten Poisson-Modell.
im
gruppierten Poisson-Modell.
- Die Nullhypothese
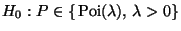 wird abgelehnt, falls
wobei
wird abgelehnt, falls
wobei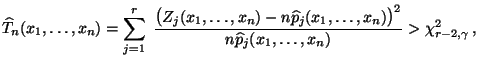
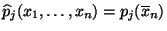 mit der in
(47)) gegebenen Funktion
mit der in
(47)) gegebenen Funktion
![$ p_j:(0,\infty)\to[0,1]$](img2427.png) und der Schätzung
und der Schätzung
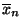 für
für 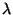 .
.
- Sei nun
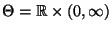 mit
mit
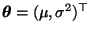 , und sei
, und sei
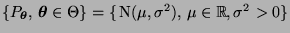 die Familie der
(eindimensionalen) Normalverteilungen.
die Familie der
(eindimensionalen) Normalverteilungen.
- Die Wahrscheinlichkeiten
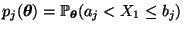 sind dann gegeben durch
sind dann gegeben durch
- Gemäß (33) genügt jeder
Maximum-Likelihood-Schätzer
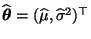 für
für
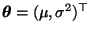 , der aus den gruppierten Daten
gewonnen wird, dem Gleichungssystem
, der aus den gruppierten Daten
gewonnen wird, dem Gleichungssystem
- Dabei ergibt sich aus (49), daß
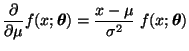 bzw.
bzw.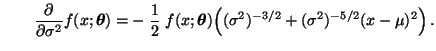
- Hieraus und aus (50) folgt, daß der ML-Schätzer
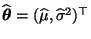 dem
folgenden Gleichungssystem genügt:
dem
folgenden Gleichungssystem genügt:
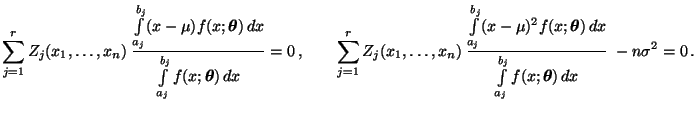
- Die erste Gleichung dieses Gleichungssystems ist äquivalent mit
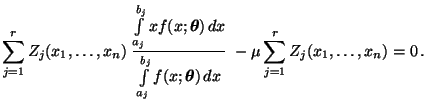
- Der ML-Schätzer
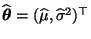 genügt
deshalb dem Gleichungssystem
das sich bei einer hinreichend großen Anzahl
genügt
deshalb dem Gleichungssystem
das sich bei einer hinreichend großen Anzahl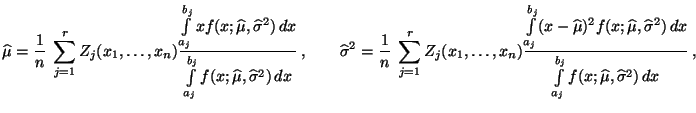
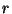 von Klassen
von Klassen
![$ (a_1,b_1],\ldots,(a_r,b_r]$](img2151.png) wie folgt näherungsweise lösen läßt:
wie folgt näherungsweise lösen läßt:
wobei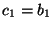 ,
,
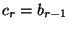 der rechte bzw. linke Endpunkt der
ersten bzw.
der rechte bzw. linke Endpunkt der
ersten bzw. 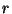 -ten Klasse und
-ten Klasse und
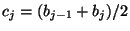 die
Klassenmittelpunkte für
die
Klassenmittelpunkte für
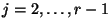 sind.
sind.
- Die Nullhypothese
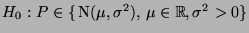 wird nun abgelehnt,
falls
wobei
wird nun abgelehnt,
falls
wobei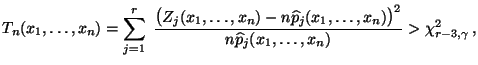
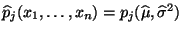 mit der in
(49)) gegebenen Funktion
mit der in
(49)) gegebenen Funktion
![$ p_j:\mathbb{R}\times(0,\infty)\to[0,1]$](img2449.png) und der in (51)
gegebenen Schätzung
und der in (51)
gegebenen Schätzung
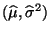 für
für
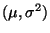 .
.
- Die Näherungslösung (51) des Gleichungssystems
(50) sollte nur dann verwendet werden, wenn die
Anzahl
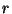 der Klassen hinreichend groß ist.
der Klassen hinreichend groß ist.
- Dies setzt einen hinreichend großen Stichprobenumfang
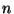 voraus.
voraus.
- Mit anderen Worten: Falls der Stichprobenumfang
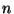 klein ist,
dann ist der
klein ist,
dann ist der 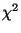 -Anpassungstest auch aus diesem Grund nicht
geeignet, um die Hypothese der Normalverteiltheit zu verifizieren.
-Anpassungstest auch aus diesem Grund nicht
geeignet, um die Hypothese der Normalverteiltheit zu verifizieren.
- Ein alternativer Test auf Normalverteilung ist der folgende Shapiro-Wilk-Test, der auch bei kleinem Stichprobenumfang
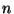 zu
akzeptablen Ergebnissen führt.
zu
akzeptablen Ergebnissen führt.
- Mit dem Shapiro-Wilk-Test können ebenfalls die Hypothesen
verifiziert werden.

- Hierfür werden die Ordnungsstatistiken
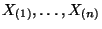 der (unabhängigen und identisch
verteilten) Zufallsvariablen
der (unabhängigen und identisch
verteilten) Zufallsvariablen
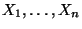 betrachtet, die
bereits in Abschnitt I.1.4 eingeführt worden sind.
betrachtet, die
bereits in Abschnitt I.1.4 eingeführt worden sind.
- Zur Erinnerung: Die Ordnungsstatistiken sind eine Klasse von
Stichprobenfunktionen, die mit Hilfe der folgenden Abbildung
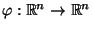 definiert werden:
definiert werden:
wobei für jedes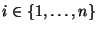
- Dabei ist die in (52) und (53)
gegebene Abbildung
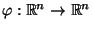 ist eine Permutation der Komponenten des Vektors
ist eine Permutation der Komponenten des Vektors
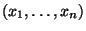 , so
daß
, so
daß
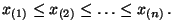
- Für jedes
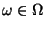 sei
die in (52) und (53) gegebene (meßbare) Permutation von
sei
die in (52) und (53) gegebene (meßbare) Permutation von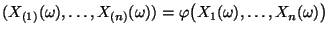
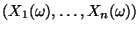 ,
so daß
,
so daß
- Die auf diese Weise definierten Zufallsvariablen
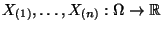 heißen die Ordnungsstatistiken von
heißen die Ordnungsstatistiken von
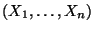 .
.
- Als Teststatistik
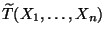 wird dabei das
Quadrat eines empirischen Korrelationskoeffizienten betrachtet,
d.h.
wird dabei das
Quadrat eines empirischen Korrelationskoeffizienten betrachtet,
d.h.
wobei der Vektor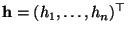 folgendermaßen
definiert wird.
folgendermaßen
definiert wird.
- Die Motivation für die Wahl dieser Teststatistik ist die Tatsache,
daß sich die Ordnungsstatistiken
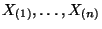 unter
unter
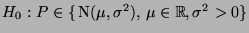 wie
folgt darstellen lassen
wie
folgt darstellen lassen
- Für jedes
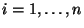 gilt nämlich
wobei
gilt nämlich
wobei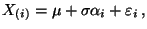
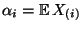 der Erwartungswert der
der Erwartungswert der 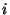 -ten
Ordnungsstatistik und
-ten
Ordnungsstatistik und
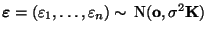 ein normalverteilter Zufallsvektor ist,
dessen Kovarianzmatrix
ein normalverteilter Zufallsvektor ist,
dessen Kovarianzmatrix
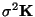 positiv definit (und damit
invertierbar) ist.
positiv definit (und damit
invertierbar) ist.
- Dabei wird dann
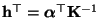 gesetzt,
wobei
gesetzt,
wobei
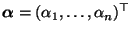 .
.
- Man kann zeigen, daß
d.h., die in (55) definierte Teststatistik
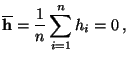
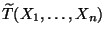 ist das Quadrat eines empirischen
Korrelationskoeffizienten.
ist das Quadrat eines empirischen
Korrelationskoeffizienten.
- Die Verteilung von
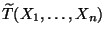 ist somit auf
dem Intervall
ist somit auf
dem Intervall ![$ [0,1]$](img2473.png) konzentriert. Sie läßt sich
(näherungsweise) durch Simulation bestimmen.
konzentriert. Sie läßt sich
(näherungsweise) durch Simulation bestimmen.
- Die Nullhypothese
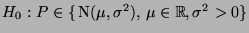 wird abgelehnt, falls
wird abgelehnt, falls
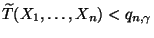 , wobei
, wobei
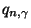 das
das 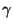 -Quantil der Verteilung von
-Quantil der Verteilung von
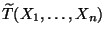 bezeichnet.
bezeichnet.
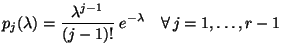 und
und