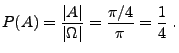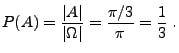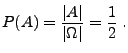Next: Bedingte Wahrscheinlichkeiten
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Einfache Urnenmodelle
Contents
Geometrische Wahrscheinlichkeiten
Während bei der Definition der Laplace'schen Wahrscheinlichkeiten,
vgl. Abschnitt 2.4.1, Quotienten von Anzahlen gebildet
werden, betrachtet man bei geometrischen Wahrscheinlichkeiten
Quotienten von Flächeninhalten bzw. Volumina.
Eine allgemeinere Variante der Definition der geometrischen
Wahrscheinlichkeit lautet wie folgt.
- Definition

- Beispiel
 (Buffonsches Nadelexperiment)
(Buffonsches Nadelexperiment)
- Das Buffonsche Nadelexperiment ist eine der ersten numerischen
Methoden, die auf stochastischen Gesetzmäßigkeiten beruht.
- Der ,,Erfinder'' ist
Georges Louis Leclerc Comte de Buffon (1707-1788).
- Heute sind solche Verfahren unter der Bezeichnung
,,Monte-Carlo-Simulation'' bekannt.
- Betrachten das System
von parallelen und äquidistanten (vertikalen) Geraden
in der euklidischen Ebene
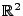 .
.
- Werfen eine Nadel mit der Länge 1
,,willkürlich'' in die Ebene
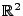 , wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
, wobei
mit ,,willkürlich'' das folgende
stochastische Modell gemeint ist.
- Betrachten die Größen
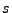 und
und 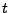 ,
die die relative Lage der Nadel bezüglich des Geradensystems
,
die die relative Lage der Nadel bezüglich des Geradensystems 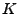 beschreiben, wobei
beschreiben, wobei
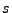 der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von
der (orthogonale) Abstand des Nadelmittelpunktes
zur nächsten linksliegenden Nachbargeraden von 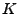 ist,
ist,
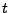 der Winkel ist, den die Nadel zum Lot auf die
Geraden von
der Winkel ist, den die Nadel zum Lot auf die
Geraden von 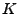 bildet.
bildet.
- Betrachten
den geometrischen Wahrscheinlichkeitsraum
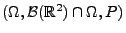 mit
mit
![$ \Omega=[0,1]\times[-\pi/2,\pi/2]$](img322.png) .
.
- Bestimmen die Wahrscheinlichkeit des
Ereignisses
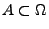 mit
dass die Nadel eine der Geraden von
mit
dass die Nadel eine der Geraden von 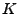 schneidet.
schneidet.
- Es gilt
d.h., für die (geometrische) Wahrscheinlichkeit des
Ereignisses 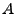 , dass die Nadel eine der Geraden von
, dass die Nadel eine der Geraden von 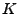 schneidet, gilt
schneidet, gilt
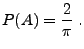 |
(12) |
- Aus der Gleichung (12)
ergibt sich nun eine Methode zur
experimentellen Bestimmung der Zahl
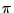 , die auf dem
sogenannten Gesetz der großen Zahlen beruht,
vgl. Abschnitt 5.2.2.
, die auf dem
sogenannten Gesetz der großen Zahlen beruht,
vgl. Abschnitt 5.2.2.
- Und zwar werfen wir die Nadel
 -mal, wobei
-mal, wobei  eine
hinreichend große natürliche Zahl sein sollte.
eine
hinreichend große natürliche Zahl sein sollte.
- Seien
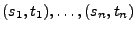 die Ergebnissse der
die Ergebnissse der  durchgeführten Nadelexperimente.
durchgeführten Nadelexperimente.
- Betrachten die Funktionswerte
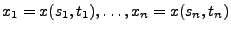 mit
d.h., die Indikatoren der Ereignisse, ob die Nadel beim
jeweiligen Wurf eine der Geraden von
mit
d.h., die Indikatoren der Ereignisse, ob die Nadel beim
jeweiligen Wurf eine der Geraden von 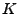 schneidet
oder nicht.
schneidet
oder nicht.
- Aus (12) und aus dem starken Gesetz der
großen Zahlen folgt dann, dass das
arithmetische Mittel
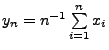 mit ,,großer Wahrscheinlichkeit'' eine gute Näherung
der Zahl
mit ,,großer Wahrscheinlichkeit'' eine gute Näherung
der Zahl 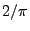 ist.
ist.
- Mit anderen Worten: Für große
 ist
ist 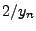 mit
großer Wahrscheinlichkeit eine gute Näherung der Zahl
mit
großer Wahrscheinlichkeit eine gute Näherung der Zahl
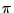 .
.
- Beachte
 Im Internet gibt es zahlreiche Seiten, wo dieses Verfahren
implementiert worden ist und mittels JAVA-Applets
auch selbst durchgeführt werden kann, vgl. beispielsweise
Im Internet gibt es zahlreiche Seiten, wo dieses Verfahren
implementiert worden ist und mittels JAVA-Applets
auch selbst durchgeführt werden kann, vgl. beispielsweise
Das folgende Beispiel soll deutlich machen, dass es (ähnlich wie
bei der Laplace'schen Wahrscheinlichkeit) auch bei der
geometrischen Wahrscheinlichkeit sehr wichtig ist, die Grundmenge
 geeignet zu wählen.
geeignet zu wählen.
- Beispiel
 (Bertrandsches Paradoxon)
(Bertrandsches Paradoxon)
- In den Kreis
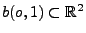 mit Mittelpunkt im Nullpunkt und
Radius Eins werde ,,auf gut Glück'' eine Sehne gelegt.
mit Mittelpunkt im Nullpunkt und
Radius Eins werde ,,auf gut Glück'' eine Sehne gelegt.
- Wie groß ist die Wahrscheinlichkeit des Ereignisses
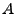 ,
dass die Sehne länger als
,
dass die Sehne länger als 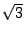 ist (wobei
ist (wobei 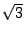 die Seitenlänge des einbeschriebenen gleichseitigen
Dreiecks ist).
die Seitenlänge des einbeschriebenen gleichseitigen
Dreiecks ist).
- Beachte: Das Problem ist ,,inkorrekt'' gestellt und
erfordert zunächst eine Präzisierung, was genau mit der
Sprechweise ,,auf gut Glück'' gemeint ist.
- Modell 1: Der Mittelpunkt der Sehne werde ,,auf gut
Glück'' in den Kreis
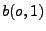 gelegt.
gelegt.
- Mit
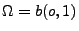 und
und
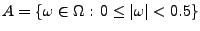 , wobei
, wobei
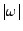 die Länge des Vektors
die Länge des Vektors 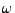 bezeichnet,
ergibt sich dann die Wahrscheinlichkeit
bezeichnet,
ergibt sich dann die Wahrscheinlichkeit
- Modell 2: Ein Endpunkt der Sehne sei fest vorgegeben, und der andere
Endpunkt werde ,,auf gut Glück'' auf die Kreislinie
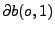 gelegt.
gelegt.
- Mit
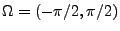 und
und
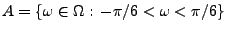 ergibt sich dann die Wahrscheinlichkeit
ergibt sich dann die Wahrscheinlichkeit
- Modell 3: Die Richtung der Sehne sei fest
vorgegeben (o.B.d.A. vertikal), und
der Mittelpunkt der Sehne werde ,,auf gut
Glück'' in das Intervall
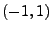 gelegt.
gelegt.
- Mit
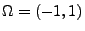 und
und
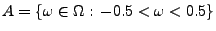 ,
ergibt sich dann die Wahrscheinlichkeit
,
ergibt sich dann die Wahrscheinlichkeit




Next: Bedingte Wahrscheinlichkeiten
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Einfache Urnenmodelle
Contents
Ursa Pantle
2004-05-10
![$\displaystyle \mathcal{B}([0,1]^2)=\sigma \Bigl( \underbrace{\{
(a,b)\times(a^\...
...^\prime),\,0<a<b<1,0<a^\prime<b^\prime<1\}
}_{\textrm{Erzeugersystem}}\Bigr)\,.$](img306.png)
![$\displaystyle P(A)=\frac{\vert A\vert}{\vert[0,1]^2\vert}=\vert A\vert\,,$](img308.png)
![$\displaystyle \mathcal{B}([0,1]^2)=\sigma \Bigl( \underbrace{\{
(a,b)\times(a^\...
...^\prime),\,0<a<b<1,0<a^\prime<b^\prime<1\}
}_{\textrm{Erzeugersystem}}\Bigr)\,.$](img306.png)
![$\displaystyle P(A)=\frac{\vert A\vert}{\vert[0,1]^2\vert}=\vert A\vert\,,$](img308.png)
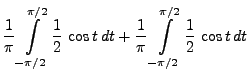
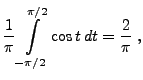
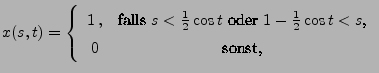
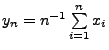 mit ,,großer Wahrscheinlichkeit'' eine gute Näherung
der Zahl
mit ,,großer Wahrscheinlichkeit'' eine gute Näherung
der Zahl ![]() geeignet zu wählen.
geeignet zu wählen.